Answers of Homework of 2022 Winter Holiday
注意,本文档仅供快速校对答案,请妥善使用
否则炮姐电死你
数学
第一张
单选题
1. A
2. C
3. C
4. B
5. C
6. D
7. D
8. D
多选题
1. A,B,D
2. B,C,A
3.A,C,D
4. A,C,A
填空题
1.
2021
已知函数f(x)在定义域(0,+∞)上是单调函数,且对任意x∈(0,+∞),都有f[f(x)﹣ ]=2,
]=2,
可设f(x)﹣ =c,故f(x)=
=c,故f(x)= +c,且f(c)=c+
+c,且f(c)=c+ =2(c>0),解可得c=1,f(x)=
=2(c>0),解可得c=1,f(x)= +1,
+1,
则f( )=2021.
)=2021.
故答案为:2021
2.

作出函数f(x)的图象,

当x≤-1时,函数f(x)= 单调递减,且最小值为f(-1)=-1,则令
单调递减,且最小值为f(-1)=-1,则令 =2,解得x=-8;当x>-1时,函数f(x)=
=2,解得x=-8;当x>-1时,函数f(x)= 在(-1,2)上单调递增,在[2,+∞)上单调递减,则最大值为f(2)=2,又f(4)=
在(-1,2)上单调递增,在[2,+∞)上单调递减,则最大值为f(2)=2,又f(4)= <2,f(-1)=-1,所求实数m的取值范围为
<2,f(-1)=-1,所求实数m的取值范围为
故答案为:

因为 的图象关于
的图象关于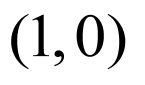 中心对称,所以
中心对称,所以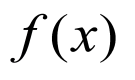 的图象关于
的图象关于 中心对称,
中心对称,
所以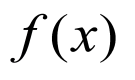 为奇函数,所以由
为奇函数,所以由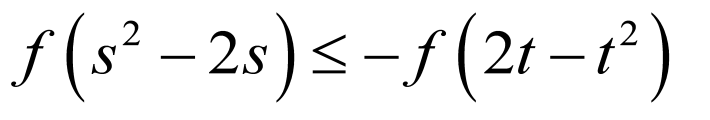 得
得 ,
,
又因为函数 是R上的减函数,
是R上的减函数,
所以 ,化简得
,化简得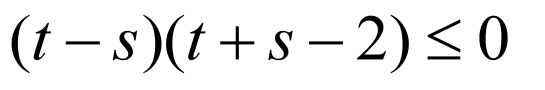 .
.
又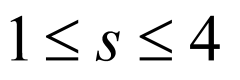 ,所以
,所以 ,
,
所以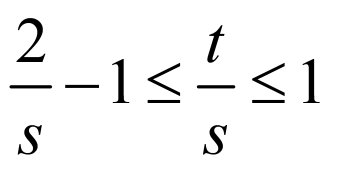 ,而
,而 ,故
,故 .
.
故答案为: .
.
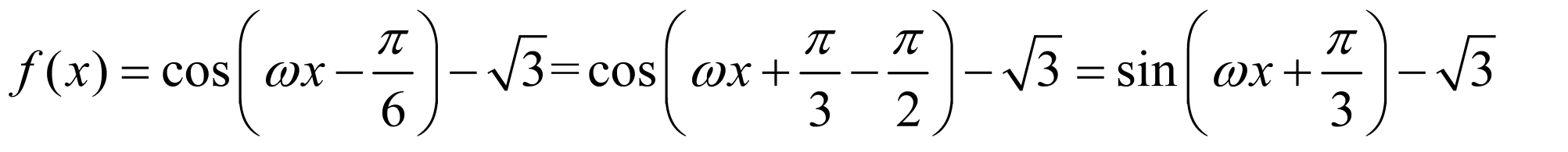 ,
,
由函数 的最小正周期为
的最小正周期为 ,又
,又 ,则
,则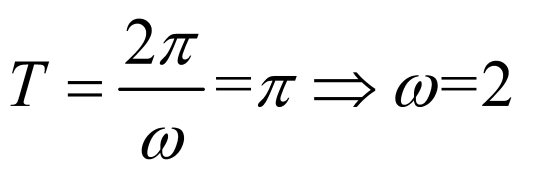 ,
,
所以函数 ;若
;若 ,则
,则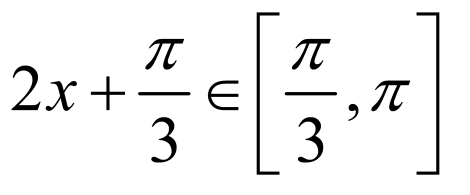 ,
,
所以 ,则
,则 ,
, ,
,
则不等式 恒成立,令
恒成立,令 ,
,
则 恒成立,
恒成立, 为开口向上的二次函数,最大值在端点处取得,
为开口向上的二次函数,最大值在端点处取得,
所以 ,则
,则 ,所以
,所以 ;
;
则实数a的取值范围是 ;
;
故答案为: .
.
1.
(1) (2)2
(2)2
【分析】
(1)将点带入,即可求解.
(2)问题转化为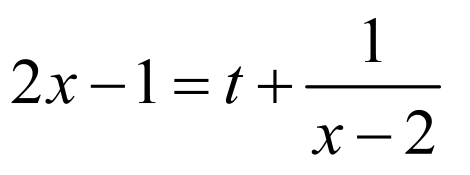 在
在 上有解,求出函数
上有解,求出函数 的最小值,即可求解.
的最小值,即可求解.
【详解】(1)由题意 解得
解得 所以
所以 .
.
(2)由(1),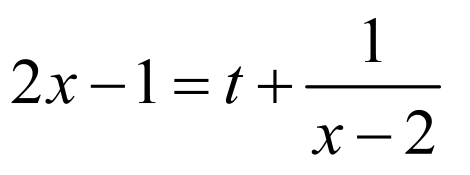 在
在 上有解,则
上有解,则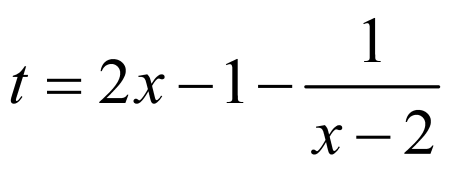
函数 在
在 严格单调递增,所以当
严格单调递增,所以当 时,
时, 取最小值2.
取最小值2.
所以 ,即:t的最小值为2.
,即:t的最小值为2.
【详解】
(1)当 时,
时, ,
,
由二次函数的性质可得 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
所以 ,
, ,
,
所以函数 的值域为
的值域为 ;
;
(2)函数 的对称轴为
的对称轴为 ,
,
当 时,函数
时,函数 在
在 上单调递增,则
上单调递增,则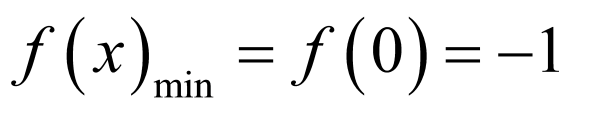 ,
,
当 时,函数
时,函数 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
则 ,
,
当 时,函数
时,函数 在
在 上单调递减,则
上单调递减,则 ,
,
综上所述;当 时,
时, ;当
;当 时,
时,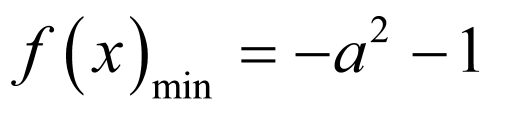 ;当
;当 时,
时, .
.
(1)若 ,则
,则 ,该函数为偶函数;
,该函数为偶函数;
若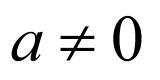 ,
, ,故
,故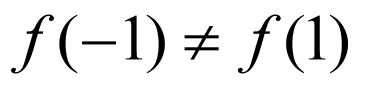 且
且 ,此时
,此时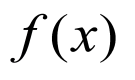 为非奇非偶函数;
为非奇非偶函数;
(2)令 ,则
,则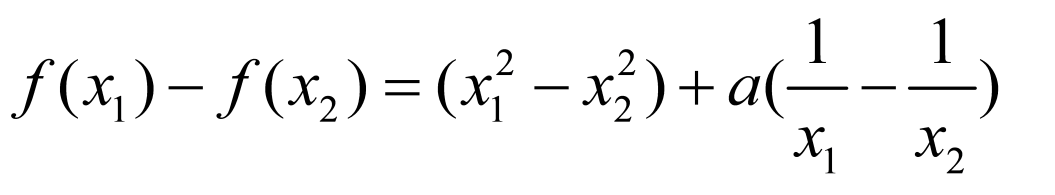
 ,
,
∵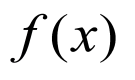 在
在 ,
, 上是增函数,∴
上是增函数,∴ ,即
,即 在
在 ,
, 上恒成立,
上恒成立,
显然 ,故
,故 ,
, 实数
实数 的取值范围为
的取值范围为 ,
, ;
;
(3) 时,
时, ,故其开口向上且对称轴为
,故其开口向上且对称轴为 ;
;
 该函数在
该函数在 ,
, 上单调递减.
上单调递减.
(1)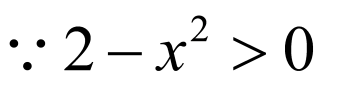 ,得
,得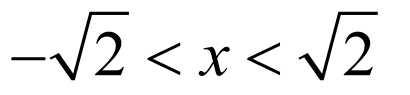
∴ 的定义域为
的定义域为 ,且
,且 ,
,
又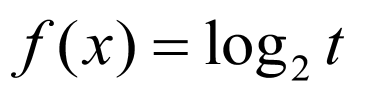 在
在 上单调递增,
上单调递增, 在
在 上单调递减
上单调递减
∴ 为偶函数且在区间
为偶函数且在区间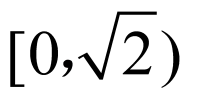 内单调递减,
内单调递减,
又 ,∴
,∴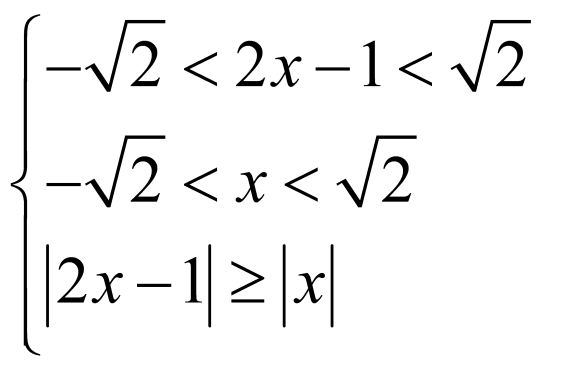 ,解得
,解得 或
或 ,
,
综上所述,原不等式的解集是 ;
;
(2)设 ,
, ,则
,则 ,即
,即
则 ,若原方程
,若原方程 有
有 个不等实根,
个不等实根,
则方程 有
有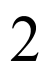 个不等实根
个不等实根 、
、 ,其中
,其中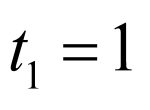 、
、 ,
,
∴ ,即
,即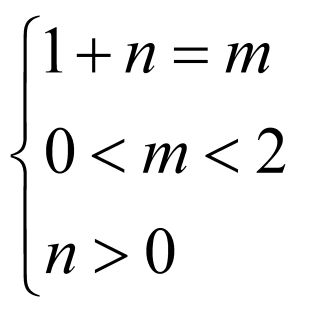 ,解得
,解得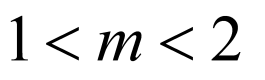 ,
,
∴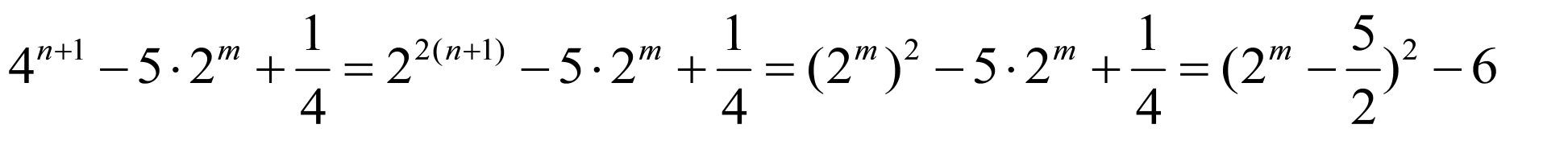 ,
,
∴当 ,即
,即 时有最小值,最小值为
时有最小值,最小值为 .
.
(1)
由题设,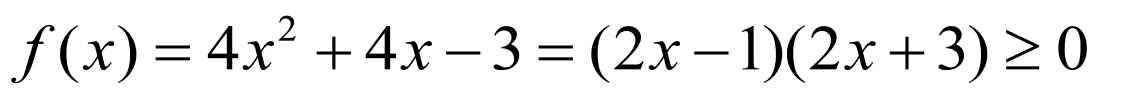 ,可得
,可得 或
或 ,
,
∴ 的解集为
的解集为 .
.
(2)
由题设,令 ,
,
当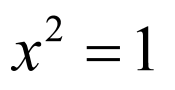 时,有两种情况:
时,有两种情况:
(1)若选①, ,则
,则 ,
, 为偶函数;
为偶函数;
又 ,
,
 不是偶函数,不合题意;
不是偶函数,不合题意;
若选②, 定义域为
定义域为 ,不关于原点对称,
,不关于原点对称, 为非奇非偶函数,不合题意;
为非奇非偶函数,不合题意;
若选③,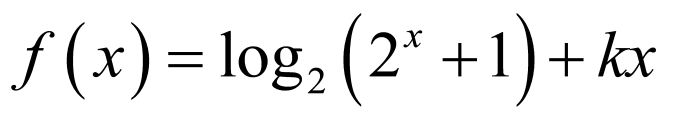 ,
,
 ,
,
若 为偶函数,则
为偶函数,则 ,
, ,解得:
,解得: ,
,
 ;
;
若选④, ,
,
 ,
,
若 为偶函数,则
为偶函数,则 ,
, ,即
,即 ;
;
 为常数,
为常数, 不恒成立,即
不恒成立,即 为偶函数不恒成立,不合题意;
为偶函数不恒成立,不合题意;
综上所述: ;
;
(2)
由(1)得: 只有一个解,
只有一个解,
整理可得: ,
,
 ,即
,即 ,
,
令 ,则
,则 ,
,
①当 时,
时, ,解得:
,解得: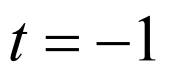 (舍);
(舍);
②当 时,
时, ,
,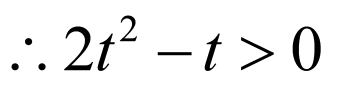 ,解得:
,解得: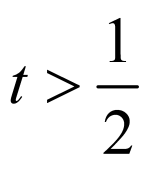 ,
,
即 在
在 上有且仅有一个解;
上有且仅有一个解;
令 ,则对称轴为
,则对称轴为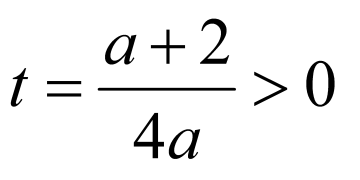 ,
,
则需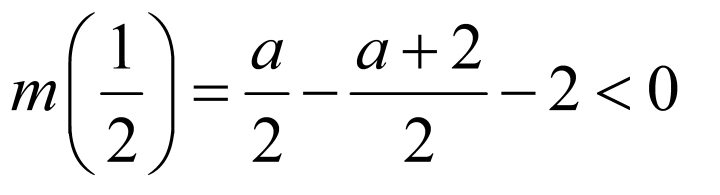 ,
,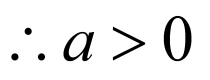 ;
;
③当 时,
时, ,
, ,解得:
,解得: ,
,
即 在
在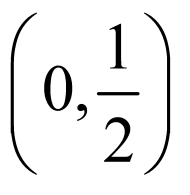 上有且仅有一个解;
上有且仅有一个解;
令 ,则对称轴为
,则对称轴为 ,
,
 ,
,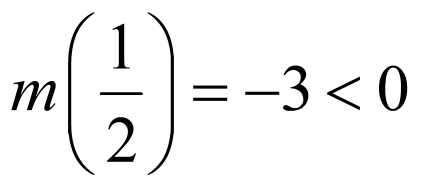 ,则需
,则需 ,解得:
,解得: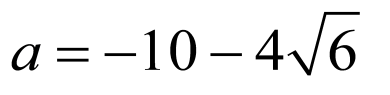 ;
;
综上所述: 的取值范围为
的取值范围为 .
.
第二张
单选题
1.
设扇形的圆心角为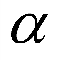 ,则
,则 ,解得:
,解得: ,即圆心角弧度数为
,即圆心角弧度数为 .
.
故选:D.
2.设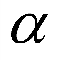 的终边上有一点
的终边上有一点 ,则
,则 ,
,
因为角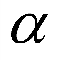 和角
和角 的终边关于y轴对称,则
的终边关于y轴对称,则 是角
是角 终边上一点,
终边上一点,
所以 .
.
故选:B.
3. D4.
解:令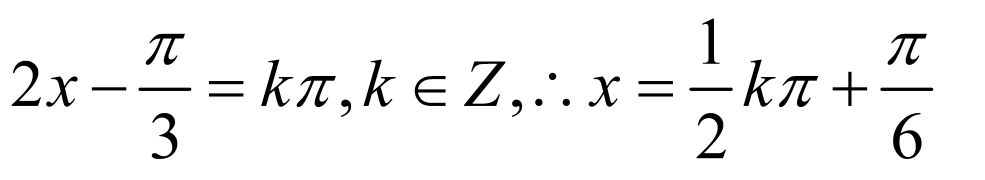 ,
,
令 ,
,
所以函数 的一个对称中心的坐标是
的一个对称中心的坐标是 .
.
故选:D
5.已知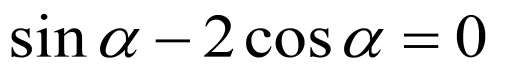 ,则
,则 ,
,

 .
.
故选:C.
6.
解:将函数 的图像所有点的横坐标缩短到原来的
的图像所有点的横坐标缩短到原来的 ,纵坐标不变,得到
,纵坐标不变,得到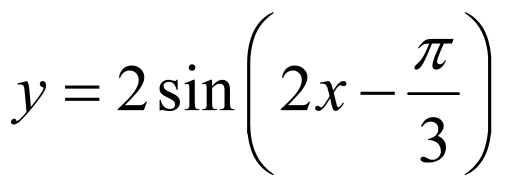 ,再把函数
,再把函数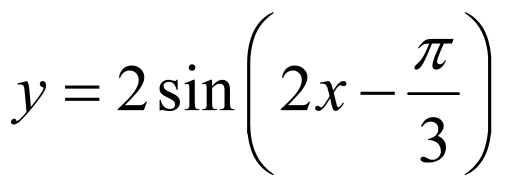 的图象向左平移
的图象向左平移 个单位长度,得到
个单位长度,得到 .
.
故选:B
7.解析: ,
,
由 得
得 ,解得
,解得 ,
,
因为 在
在 内有零点,所以
内有零点,所以 ,
,
解得 ,又由
,又由 在
在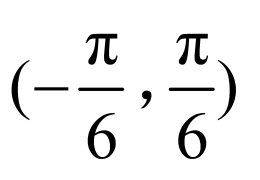 上单调递减,
上单调递减,
解得 ,所以
,所以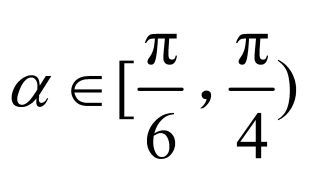 ,
,
故选:C.
8.将 的图向左平移
的图向左平移 个单位长度
个单位长度 ,再将
,再将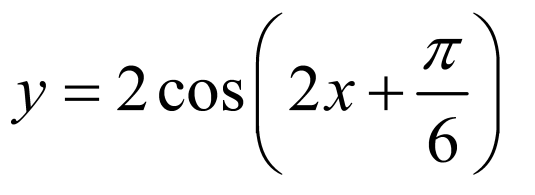 图象上各点的横坐标伸长为原来的
图象上各点的横坐标伸长为原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数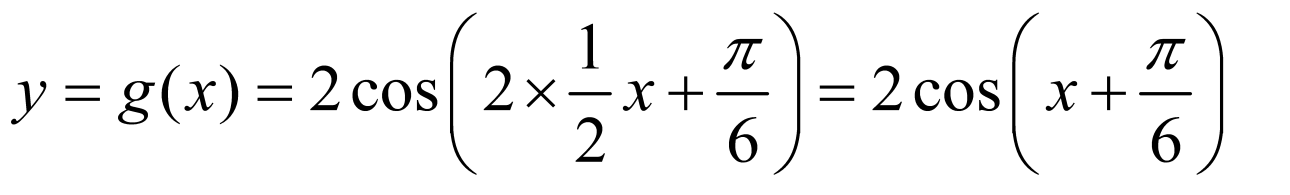 ,所以
,所以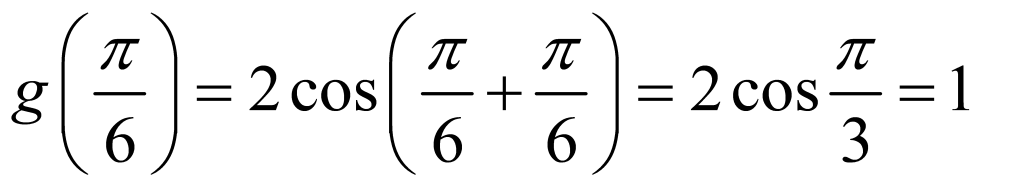 .
.
故选:C.
多选题1.
由图可知, ,
, ,故
,故 ,A正确;
,A正确;
则 ,
,
又 ,得
,得 ,
,
因为 ,
, ,C正确;
,C正确;

因为 ,故
,故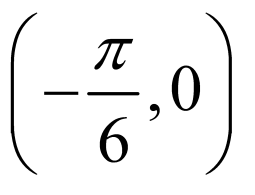 不是函数
不是函数 的一个对称中心,B错误;
的一个对称中心,B错误;
当 时,
时, ,函数
,函数 在
在 上不是单调函数,所以函数
上不是单调函数,所以函数 在区间
在区间 上也不是单调函数,D错误.
上也不是单调函数,D错误.
故选:AC.
2.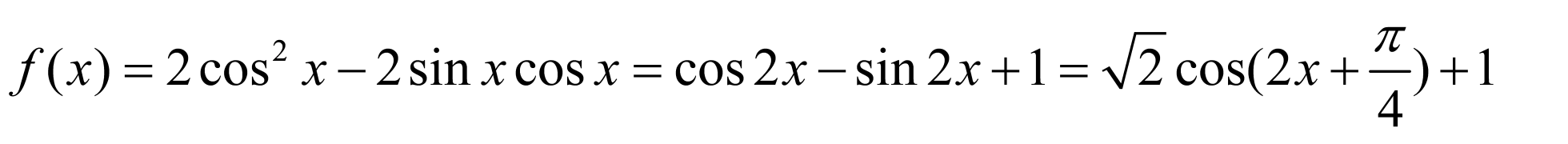 ,
,
∴ 最大值为
最大值为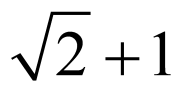 ,最小正周期为
,最小正周期为 ,A错误,B正确;
,A错误,B正确;
由 关于
关于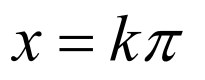 对称,令
对称,令 ,则
,则 ,当
,当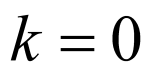 时
时 ,C正确;
,C正确;
由 在
在 递减,令
递减,令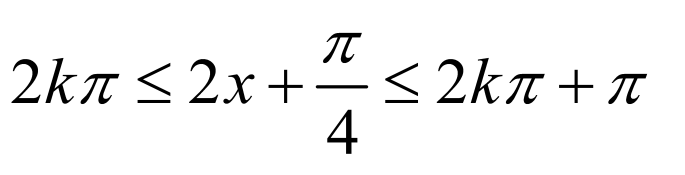 ,有
,有 ,易知
,易知
 ,D错误.
,D错误.
故选:BC
3.
解:由函数的图像可知, 的图像过点
的图像过点 ,
,
所以 ,可得
,可得 ,
,
因为 ,所以
,所以 ,
,
因为 的图像过点
的图像过点 ,
,
所以 ,解得
,解得 ,
,
所以 ,
,
因为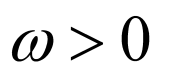 ,所以不妨设
,所以不妨设 ,则可得
,则可得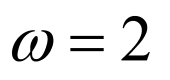 ,
,
所以 ,
,
因为 ,
,
所以 ,
,
因为对于任意的 ,
,
所以 ,
,
所以 ,
,
所以 ,
,
当 时,
时, ,
,
当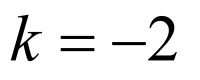 时,
时, ,
,
故选:CD
4.解: 摩天轮
摩天轮 转一圈,
转一圈,
 在
在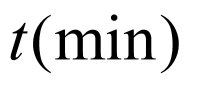 内转过的角度为
内转过的角度为 ,
,
建立平面直角坐标系,如图,
设 是以
是以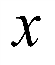 轴正半轴为始边,
轴正半轴为始边, 表示点
表示点 的起始位置
的起始位置 为终边的角,
为终边的角,
以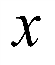 轴正半轴为始边,
轴正半轴为始边, 为终边的角为
为终边的角为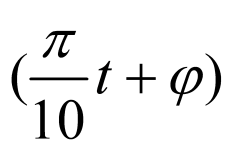 ,
,
即点 的纵坐标为
的纵坐标为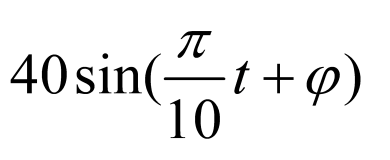 ,
,
又由题知, 点起始位置在最高点处,
点起始位置在最高点处,


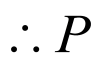 点距地面高度
点距地面高度 关于旋转时间
关于旋转时间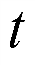 的函数关系式为:
的函数关系式为:
即
当 时,
时, ,故A正确;
,故A正确;
若摩天轮转速减半, ,则其周期变为原来的2倍,故B错误;
,则其周期变为原来的2倍,故B错误;
第
 点距安地面的高度为
点距安地面的高度为
第
 点距离地面的高度为
点距离地面的高度为
第 和第
和第 时
时 点距离地面的高度相同,故C正确;
点距离地面的高度相同,故C正确;
摩天轮转动一圈, 点距离地面的高度不低于
点距离地面的高度不低于 ,
,
即 ,
,
即 ,
, ,
,
得 ,
,

 或
或 ,
,
解得 或
或 ,
,
共 ,故D错误.
,故D错误.
故选:AC.
1.
解:因为 ,所以
,所以 ,所以
,所以 ,当
,当 时
时 ,当
,当 时
时 ,函数图象如下所示:
,函数图象如下所示:

方程 在
在 上有两个不同的解,即方程
上有两个不同的解,即方程 在
在 上有两个不同的解,即
上有两个不同的解,即 与
与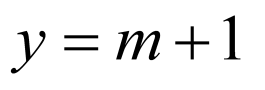 有两个不同的交点,所以
有两个不同的交点,所以 ,解得
,解得 ,即
,即
故答案为:
∵
 ,
,
∴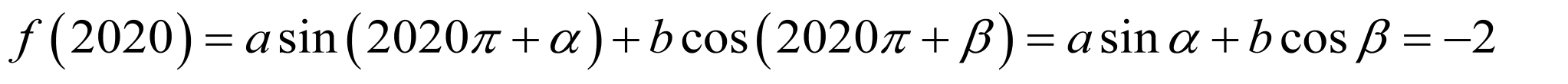 .
.
故答案为:
 ,因为
,因为 ,
, ,故
,故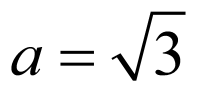 ,原式为
,原式为 ,当
,当 取到最大值时,
取到最大值时, ,当
,当 ,
, 取得前两次最大值时,
取得前两次最大值时,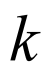 分别为0和1,
分别为0和1, 时,
时, ,
, ,此时需满足
,此时需满足 ,解得
,解得 .
.
故答案为:
(1)依题意, ,
, ,
, ,
,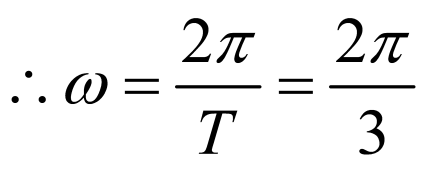 ,又
,又 ,
, ;
;
 ;
;
 ,
,
即第2018min时点P所在位置的高度为70m;
(2)由(1)知, ;
;
依题意: ,
, ,
, ,
,
解得 ,
, ,即
,即 ,
, ;
;
 ,
, 转一圈中有0.5min时间可以看到公园全貌.
转一圈中有0.5min时间可以看到公园全貌.
故10圈中有5min时间可以看到公园全貌.
解答题1.
:根据题意,可得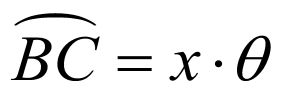 ,
, .
.
又 ,
,
所以 ,所以
,所以 .
.
(2)
解:依据题意,可知 ,
,
化简得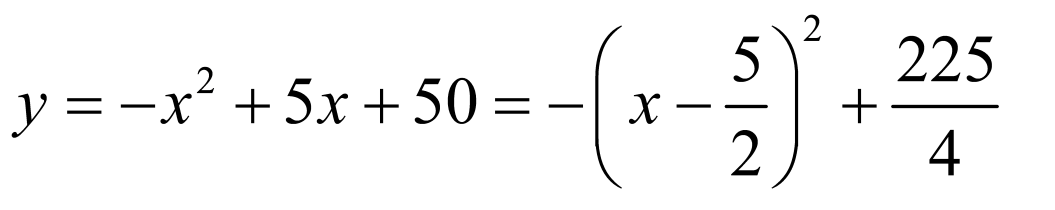 .
.
于是,当 (满足条件
(满足条件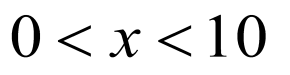 )时,
)时, .
.
所以当 时铭牌的面积最大,且最大面积为
时铭牌的面积最大,且最大面积为 .
.
(Ⅰ)因为 ,
, ,
,
所以 ,
,
即
所以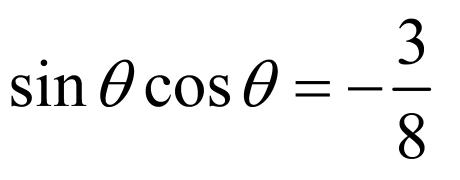
(Ⅱ)由上知,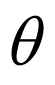 为第二象限的角,
为第二象限的角,
所以 ,
,
所以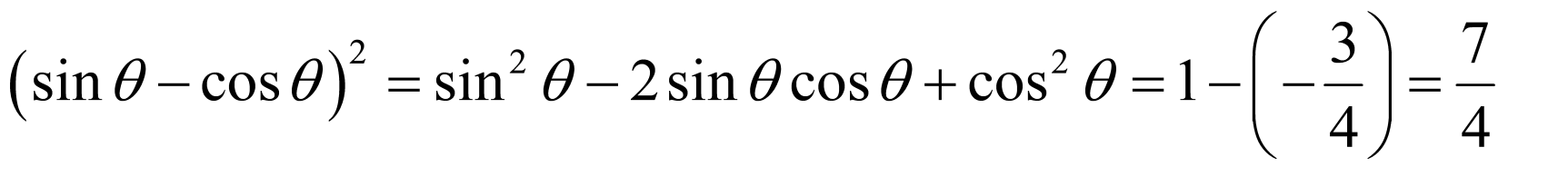 ,
,
所以
(1)由题意可知,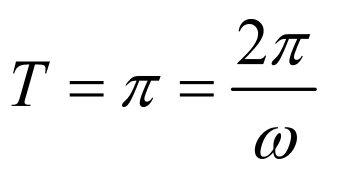 ,得
,得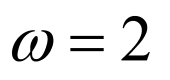 .
.
又因为 为函数
为函数 的一个零点,所以
的一个零点,所以 ,
,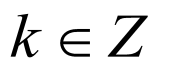 ,
,
所以 ,
,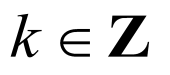 .又因为
.又因为 ,所以
,所以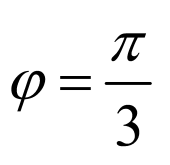 ,
,
所以 .
.
(2)若 单调递增,则满足
单调递增,则满足 ,
,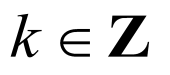 ,
,
解得 ,
,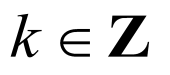 ,
,
当时 ,
,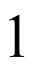 得
得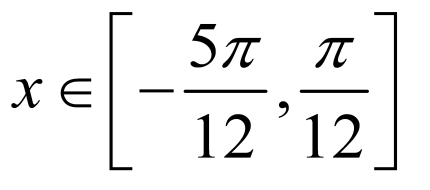 ,
,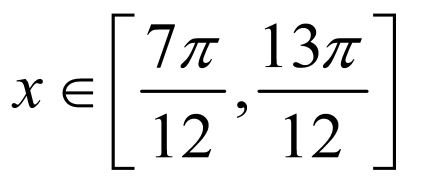 ,
,
又因为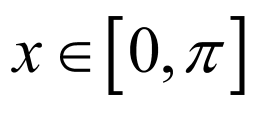 ,交集为
,交集为 ,
,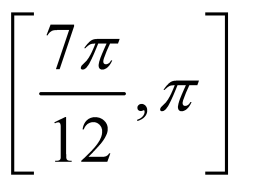 ,
,
所以 在
在 上的单调递增区间为
上的单调递增区间为 ,
,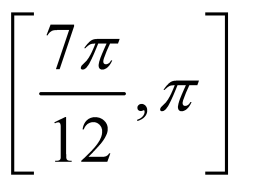 .
.
(1)解:∵函数
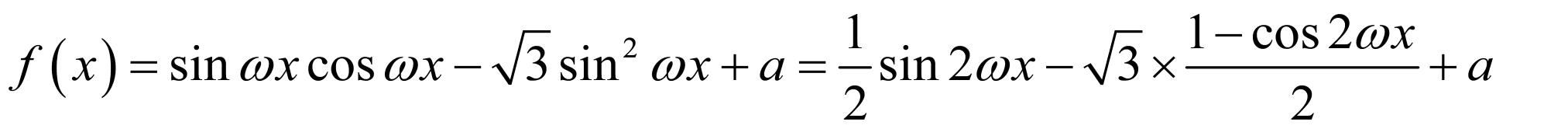
 ,且
,且 是最大值,
是最大值,
∴ ,
,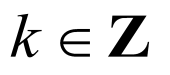 .
.
解得 ,
,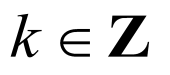 ,故
,故 的最小值为
的最小值为 ,
,
故 .
.
(2)
解:如果 在区间
在区间 上的最小值为
上的最小值为 ,
,
因为 ,所以
,所以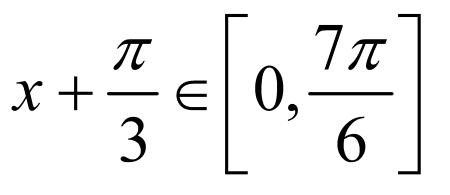 ,
,
∴当 时,函数
时,函数 取得最小值为
取得最小值为 ,
,
解得 .
.
(1):由图象得 ,
,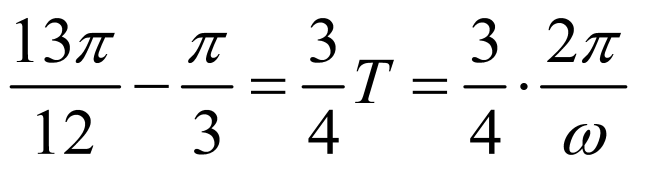 ,所以
,所以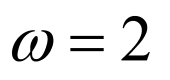 ,
,
由 ,所以
,所以 ,
,
 ,
,
 ,
,
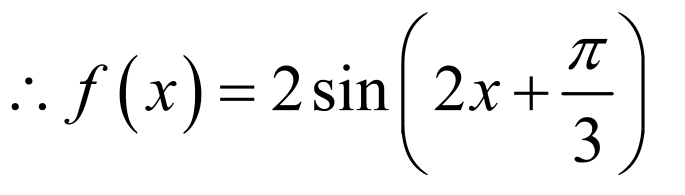
(2)
解:将函数 的图象上每一点横坐标缩短为原来的
的图象上每一点横坐标缩短为原来的 ,得到
,得到 ,再将
,再将 向右平移
向右平移 个单位得到
个单位得到 ,最后再向上平移
,最后再向上平移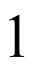 个单位得到
个单位得到 ,即
,即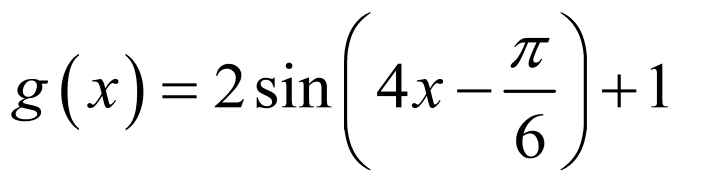
当 时,所以
时,所以 ,所以
,所以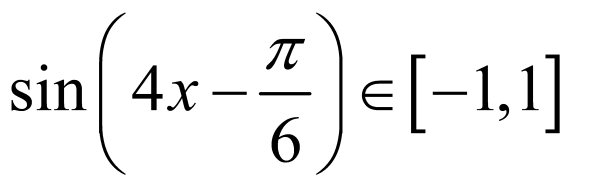 ,
,

(1)由题设的数据可得 ,故
,故 ,
,
而 ,故
,故 ,故
,故 ,
,
其中振幅为3, .
.
(2)令 ,则
,则 ,其中
,其中
故 或
或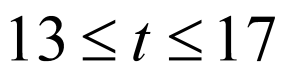 ,故船舶至多能在港内停留
,故船舶至多能在港内停留 小时.
小时.
第三张
单选题
1.
在正方体 中,
中, ,
,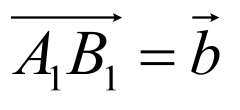 ,
,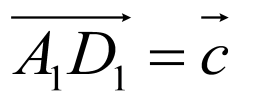 ,O为底面ABCD的中心,G为
,O为底面ABCD的中心,G为 的重心,连接OG,
的重心,连接OG,
则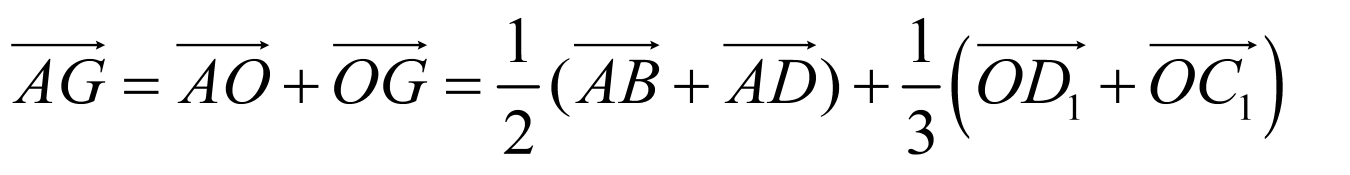

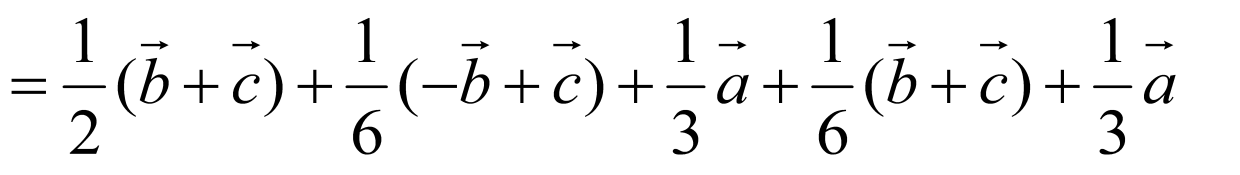
 .
.
故选:A.
2.
P∈平面ABC,若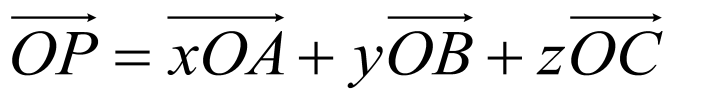 则x+y+z=1.
则x+y+z=1.
 .又动点Q在
.又动点Q在 所在平面内运动,
所在平面内运动,
所以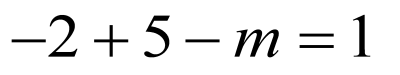 ,解得
,解得 .
.
故选:B
3.因为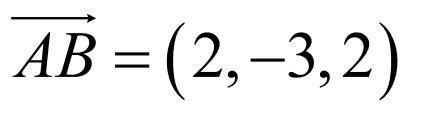 ,
, ,
, ,且
,且 ,
,
所以 ,所以
,所以 ,解得
,解得
故选:C
4.设 ,由题意得:
,由题意得: ,
,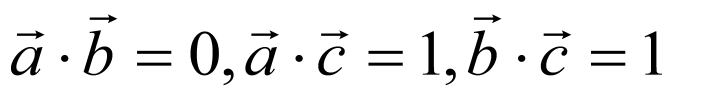 ,
,
 .
.
故选:B.
5.
对于A,因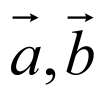 分别是直线
分别是直线 的方向向量,且
的方向向量,且 ,直线
,直线 所成的角为
所成的角为 ,则
,则 ,A正确;
,A正确;
对于B,D,因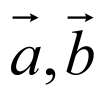 分别是直线l的方向向量与平面
分别是直线l的方向向量与平面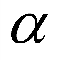 的法向量,且
的法向量,且 ,直线l与平面
,直线l与平面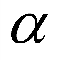 所成的角为
所成的角为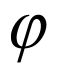 ,
,
则有 ,B错误,D正确;
,B错误,D正确;
对于C,因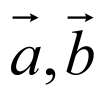 分别是平面
分别是平面 的法向量,且
的法向量,且 ,平面
,平面 所成的角为
所成的角为 ,
,
则 不大于
不大于 ,
, ,C正确.
,C正确.
故选:B
6. ,
, ,又
,又 与
与 互相垂直,
互相垂直,
 ,解得:
,解得: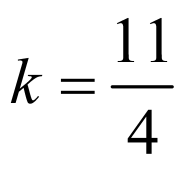 .
.
故选:D.
7.正方体 的棱上到直线
的棱上到直线 与
与 的距离相等的点分别为:
的距离相等的点分别为: ,
, 的中点,
的中点, 的四等分点(靠近
的四等分点(靠近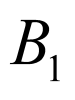 ),
),
假设 与
与 重合,
重合, 的中点为
的中点为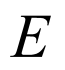 ,
, 的四等分点(靠近
的四等分点(靠近 )为
)为 ,
,
如图,以 为坐标原点,
为坐标原点, ,
, ,
, 所在直线分别为
所在直线分别为 ,
, ,
, 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,

设 ,则
,则 ,
, ,
, ,
, ,
,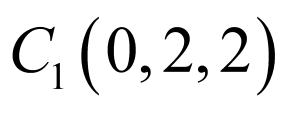 ,
,
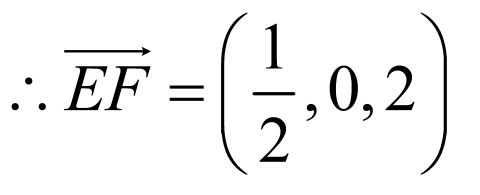 ,
, ,
,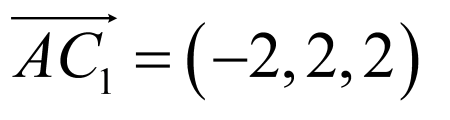 ,
,
设平面 的法向量
的法向量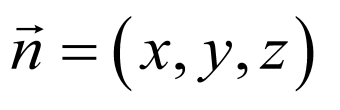 ,
,
则 ,即
,即 ,
,
取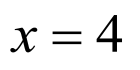 ,得
,得 ,
,
设直线 与平面
与平面 所成角为
所成角为 ,则直线
,则直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,
,
故选:D.
8.
如图所示:以 为
为 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设 ,
,
则 ,
, ,
, ,
,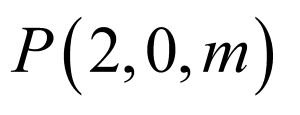 ,
, ,
,
设平面 的法向量为
的法向量为 ,则
,则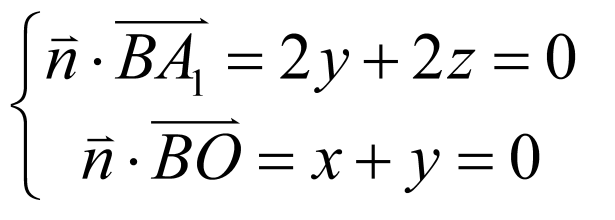 ,
,
取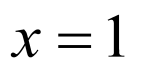 得到
得到 ,
,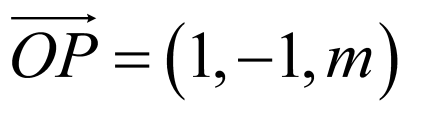 ,
,
直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为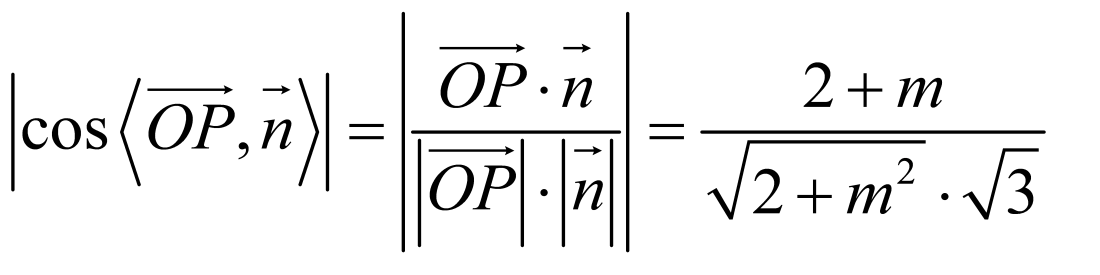 ,
,
设 ,则
,则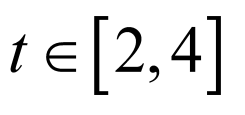 ,
,
 ,
,
当 时,有最大值为
时,有最大值为 ,当
,当 时有最小值为
时有最小值为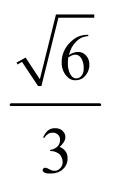 .
.
故选:A.

1.
当 ,满足
,满足 与
与 共线,
共线, 与
与 共线,而
共线,而 与
与 不一定共线,A错误;若
不一定共线,A错误;若 与
与 均为零向量时,能够保证
均为零向量时,能够保证 ,则存在无数多的实数
,则存在无数多的实数 ,使
,使 ,B错误;因为
,B错误;因为 ,即
,即 ,故
,故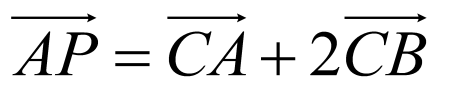 ,由平面向量基本定理可得:P,A,B,C四点共面,C正确;因为非零空间向量
,由平面向量基本定理可得:P,A,B,C四点共面,C正确;因为非零空间向量 满足
满足 ,故
,故 ,所以
,所以 ,D正确.
,D正确.
故选:AB
2.
根据题意,若 与
与 共线,则有
共线,则有 ,
,
无解,即两个向量不会共线,
若 与
与 的夹角为钝角,必有
的夹角为钝角,必有 ,
,
解可得: ,分析选项:
,分析选项: 、2、3符合,
、2、3符合,
故选:ABC.
3.
根据题意,若 与
与 共线,则有
共线,则有 ,
,
无解,即两个向量不会共线,
若 与
与 的夹角为钝角,必有
的夹角为钝角,必有 ,
,
解可得: ,分析选项:
,分析选项: 、2、3符合,
、2、3符合,
故选:ABC.
4.
选项A,因为 ,所以
,所以 共面;
共面;
选项B,因为 ,所以
,所以 共面;
共面;
选项C, 在
在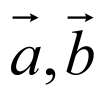 构成的平面内,
构成的平面内, 不在这个平面内,不符合.
不在这个平面内,不符合.
选项D,因为 共线,所以
共线,所以 共面.
共面.
故选:ABD
5.
对于A中,如图所示,连接 交于点
交于点 ,连接
,连接 ,
,
因为 为正三棱柱,所以其侧面都是矩形,所以
为正三棱柱,所以其侧面都是矩形,所以 为
为 的中点,
的中点,
又因为 是
是 的中点,所以
的中点,所以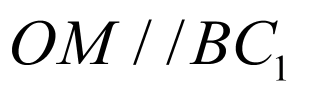 ,
,
由 平面
平面 ,且
,且 平面
平面 ,所以
,所以 平面
平面 ,所以A正确;
,所以A正确;
对于B中,因为 交
交 于点
于点 ,
,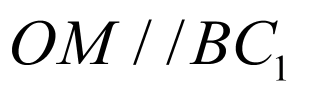 ,
, ,所以
,所以 ,
,
因为 与
与 与平面
与平面 成角相等,所以
成角相等,所以 和
和 到平面
到平面 的距离相等,
的距离相等,
所以B正确;
对于C中,假设存在点 ,使得
,使得 平面
平面 ,
,
因为 平面
平面 ,所以
,所以 ,
,
令 ,可得
,可得 ,
,
因为 和
和 所成角为锐角,
所成角为锐角, 和
和 所成角为锐角,
所成角为锐角,
所以 ,所以
,所以 ,
,
所以 不成立,所以C错误;
不成立,所以C错误;
对于D中,由C知 ,所以不存在点
,所以不存在点 ,使得
,使得 ,所以D错误.
,所以D错误.
故选:AB.

1.




1.
(1)
在三棱柱中, 平面
平面
由 ,
, ,
,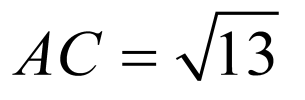 ,得
,得 ,
,
由勾股定理知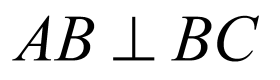 ,
,

(2) 平面
平面 ,以
,以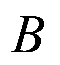 为原点,
为原点, 为
为 轴,
轴, 为
为 轴,
轴, 为
为 轴,建立空间直角坐标系,如图,
轴,建立空间直角坐标系,如图,

则 ,
, ,
, ,
,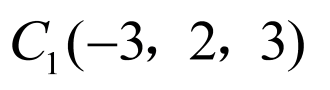 .
.
在平面 中,
中, ,
, .
.
设法向量 ,则
,则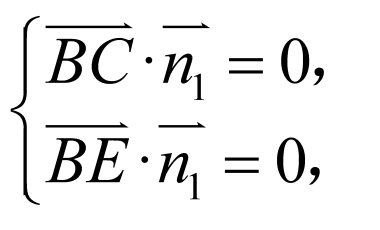 即
即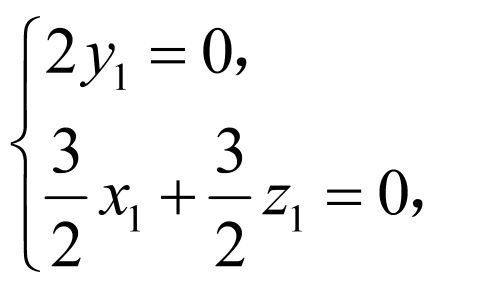
取
在平面 中,
中, ,
, .
.
设法向量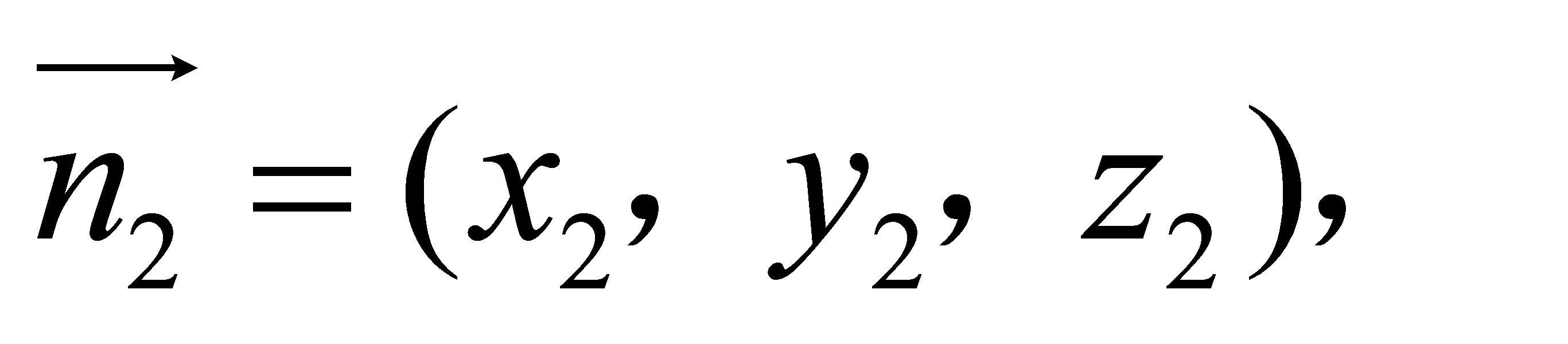 则
则 即
即
取
于是: ,
,
又二面角 为锐角,故所求二面角的余弦值为
为锐角,故所求二面角的余弦值为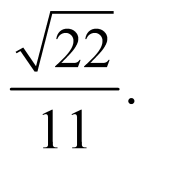
(1)连接 交
交 于
于 ,进而证明
,进而证明 ,然后根据线面平行的判定定理证明问题;
,然后根据线面平行的判定定理证明问题;
(2)建立空间直角坐标系,求出平面 的法向量,进而通过空间向量的夹角公式求得答案;
的法向量,进而通过空间向量的夹角公式求得答案;
(3)求出平面 的法向量,结合(2),进而通过空间向量的夹角公式求得答案.
的法向量,结合(2),进而通过空间向量的夹角公式求得答案.
(1)
证明:连接 ,与
,与 交于
交于 ,则
,则 为
为 的中点,又
的中点,又 分别为
分别为 的中点,∴
的中点,∴ ,∵
,∵ 平面
平面 ,
, 平面
平面 ,∴
,∴ 平面
平面 .
.
(2)
设 是
是 的中点,连接
的中点,连接 ,∵
,∵ 是正方形,
是正方形, 为正三角形,∴
为正三角形,∴ .又∵面
.又∵面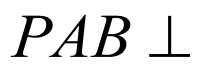 面
面 ,交线为
,交线为 ,∴
,∴ 平面
平面 .
.
以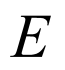 为原点,分别以
为原点,分别以 ,
, ,
, 所在直线为
所在直线为 ,
, ,
, 轴,如图,建立空间直角坐标系
轴,如图,建立空间直角坐标系 ,则
,则 ,
,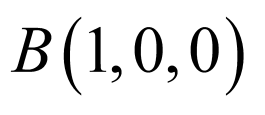 ,
, ,
, ,
, ,
, ,
, ,∴
,∴ ,
, ,
,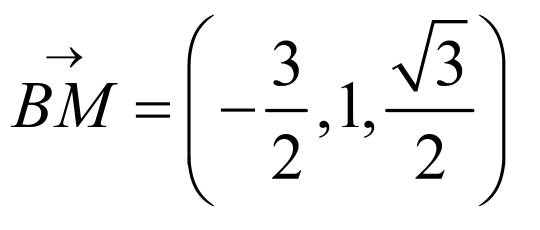
设平面 的法向量为
的法向量为 ,则
,则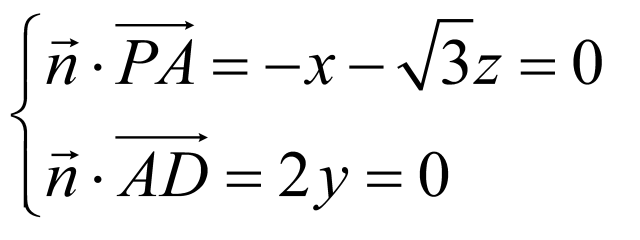 ,令
,令 .则
.则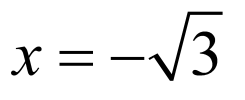 ,得
,得 .设直线
.设直线 与平面
与平面 所成角为
所成角为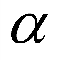 ,
,
∴ ,即直线
,即直线 与平面
与平面 所成角的正弦值
所成角的正弦值 .
.
(3)
由(2)可知 ,设平面
,设平面 的法向量为
的法向量为 ,则
,则
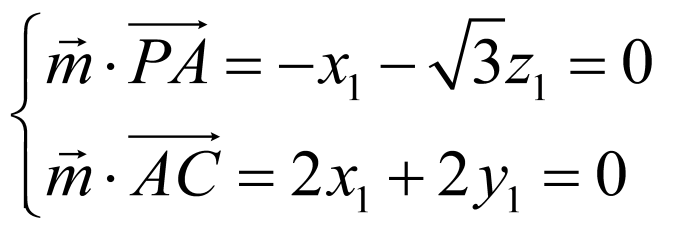 ,令
,令 .则
.则 ,
,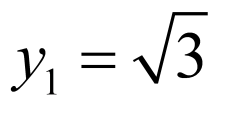 ,
, .
.
设面 与面
与面 夹角为
夹角为 ,∴
,∴ ,∴面
,∴面 与面
与面 夹角的余弦值为
夹角的余弦值为 .
.
(1)
设 ,
,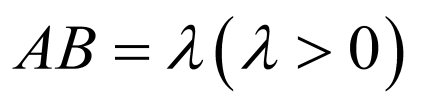 ,如图,以
,如图,以 为坐标原点,
为坐标原点,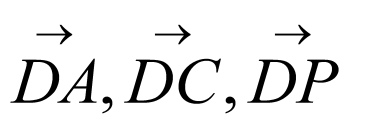 所在方向分别为
所在方向分别为 ,
, ,
, 轴的正半轴,建立空间直角坐标系.
轴的正半轴,建立空间直角坐标系.
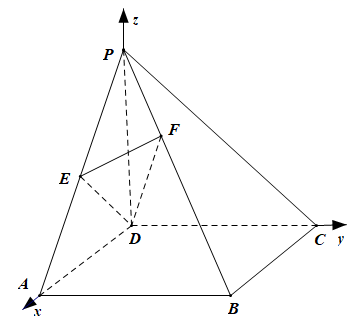
则 ,
, ,
, ,
, ,因为点
,因为点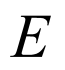 是
是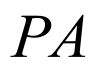 的中点,所以
的中点,所以 ,
,
 ,
, ,于是
,于是 ,即
,即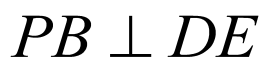 ,又已知
,又已知 ,而
,而 ,所以
,所以 平面
平面 .
.
(2)
由 平面
平面 ,所以
,所以 是平面
是平面 的一个法向量;
的一个法向量;
由(1)知, 平面
平面 ,所以
,所以 是平面
是平面 的一个法向量.
的一个法向量.
若面 与面
与面 所成二面角的大小为
所成二面角的大小为 ,则
,则 ,解得
,解得 .所以
.所以 ,故当面
,故当面 与面
与面 所成二面角的大小为
所成二面角的大小为 时,
时, .
.
(1)
因为 平面ABC,又因为
平面ABC,又因为 ,即
,即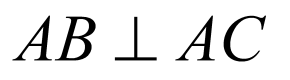 ,以A为坐标原点,分别以AB,AC,
,以A为坐标原点,分别以AB,AC, 所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系.
所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系.

因为 ,
, ,所以
,所以 ,
, ,
, ,
,
则 ,
, ,
,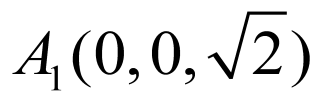 ,
, ,
,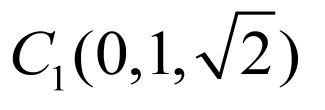 ,
,
所以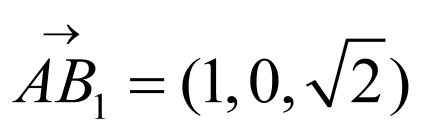 ,
, ,
,
所以 ,
,
所以 .
.
(2)
由(1)知 ,
,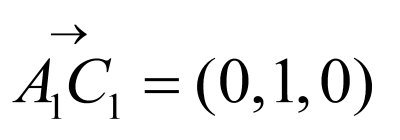 ,
, ,
,
设平面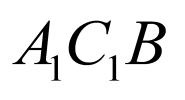 的法向量为
的法向量为 ,
,
 ,令
,令 ,则
,则 ,
,
所以点A到平面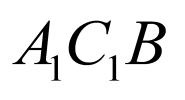 的距离为
的距离为 .
.
(1)
因为 平面ABC,又因为
平面ABC,又因为 ,即
,即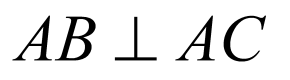 ,以A为坐标原点,分别以AB,AC,
,以A为坐标原点,分别以AB,AC, 所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系.
所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系.

因为 ,
, ,所以
,所以 ,
, ,
, ,
,
则 ,
, ,
,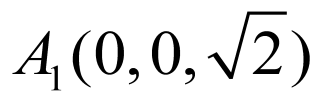 ,
, ,
,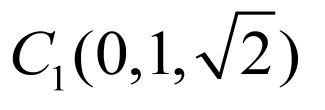 ,
,
所以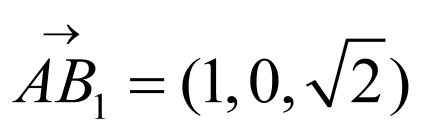 ,
, ,
,
所以 ,
,
所以 .
.
(2)
由(1)知 ,
,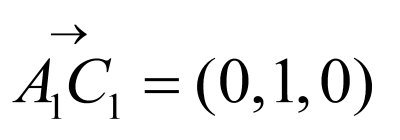 ,
, ,
,
设平面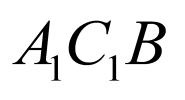 的法向量为
的法向量为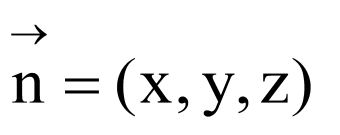 ,
,
 ,令
,令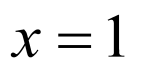 ,则
,则 ,
,
所以点A到平面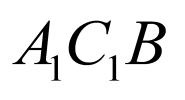 的距离为
的距离为 .
.
(1)取 的中点
的中点 ,连接
,连接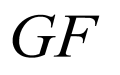 ,
, ,如图,
,如图,

因为 平面
平面 ,
, 平面
平面 ,
,
所以 ,
,
∴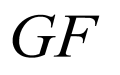 为三角形
为三角形 的中位线,
的中位线,
∴ ,
, ,
,
∴四边形 为平行四边形,
为平行四边形,
∴ ,又
,又 平面
平面 ,
, 平面
平面 ,
,
∴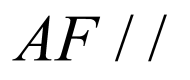 平面
平面 .
.
(2)∵ ,
, 为
为 的中点,
的中点,
∴ ,又
,又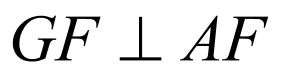 ,
,
∴ 平面
平面 ,
,
∵ ,∴
,∴ 平面
平面 ,又
,又 平面
平面 ,
,
∴
平面 平面
平面 ;
;
(1)延长 交于点
交于点 ,由
,由 ,可得点
,可得点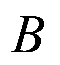 是线段
是线段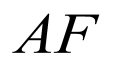 中点,则有
中点,则有 ,即可证得结果.
,即可证得结果.
(2)作 于
于 ,连
,连 ,由
,由 ,可知
,可知 ,则
,则 ,建立空间直角坐标系,求得平面
,建立空间直角坐标系,求得平面 的法向量
的法向量 计算
计算 即可得出结果.
即可得出结果.
(1)
证明:延长 交于点
交于点 ,
,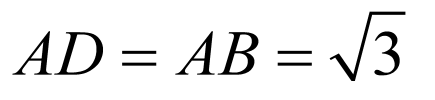 ,
,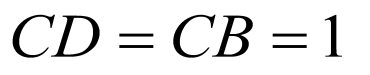 ,
,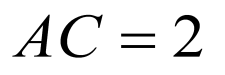 ,则
,则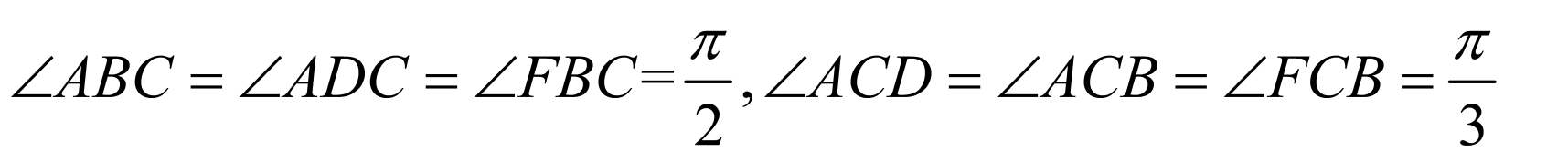 ,
,
所以 ,所以点
,所以点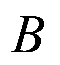 是线段
是线段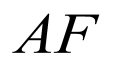 中点,
中点,
又因为点 为线段
为线段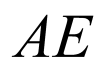 中点,所以
中点,所以 ,
,
因为 ,
, ,
,
所以 平面
平面 .
.
(2)
作 于
于 ,连
,连 ,
,
因为 ,所以
,所以 ,
,
所以 ,如图建立空间直角坐标系,
,如图建立空间直角坐标系,
 ,
, ,
,
 ,
,
 ,
,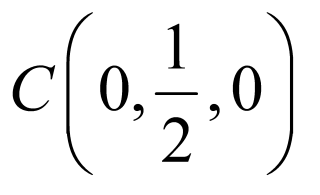 ,
,
 ,
, ,
, ,
,
设平面 的法向量是
的法向量是 ,
,
则有 ,即
,即 ,
, ,
, ,
,
 ,
,
直线 与平面
与平面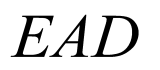 所成角的正弦值为
所成角的正弦值为 .
.

第四张
单选题
1.
由已知条件可得 ,解得
,解得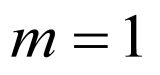 .故选:B.
.故选:B.
解:因为双曲线 的离心率不大于
的离心率不大于 ,
,
所以 解得:0<m≤1.故选:B.
解得:0<m≤1.故选:B.
因为直线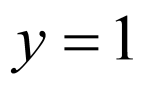 与
与 在第一象限的交点为
在第一象限的交点为 ,所以点
,所以点 的纵坐标为1,
的纵坐标为1,
抛物线 的准线方程为:
的准线方程为: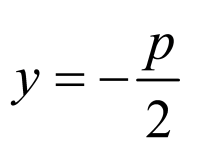 ,因为
,因为 ,所以有
,所以有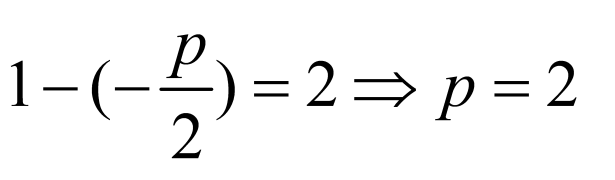 ,
,
由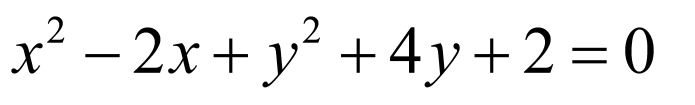 ,得
,得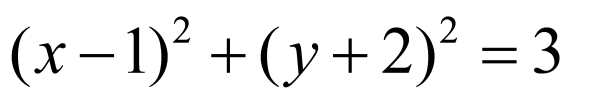 ,则圆心为
,则圆心为 ,半径
,半径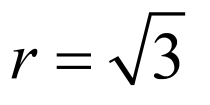 ,
,
因为圆心 到直线
到直线 的距离为
的距离为 ,且
,且 ,
,
所以圆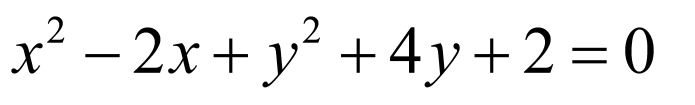 到直线
到直线 的距离为
的距离为 的点有2个,故选:B
的点有2个,故选:B
抛物线 化为
化为 ,可得焦点
,可得焦点 ,准线方程为
,准线方程为 ,如图所示,
,如图所示,

可得动点P到直线l∶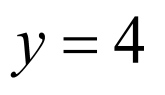 的距离为
的距离为 ,
,
又由 ,从而
,从而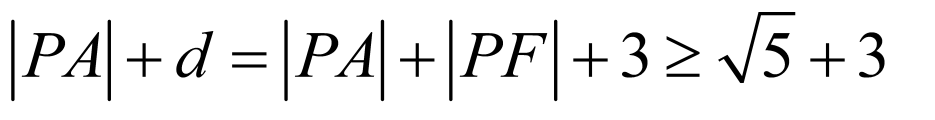 .
.
所以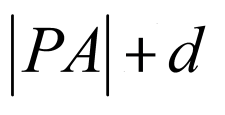 的最小值等于
的最小值等于 .故选:D.
.故选:D.
设点 ,则
,则 ,所以,
,所以, ,解得
,解得 ,
,
在双曲线 中,
中, ,
, ,
, ,所以,
,所以,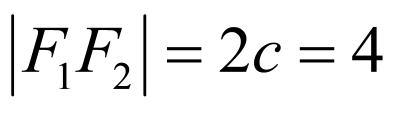 ,
,
因此, .故选:D.
.故选:D.
由基本不等式及椭圆定义可知 ,
, 的最大值为
的最大值为 ,由题意知
,由题意知 ,
, ,
,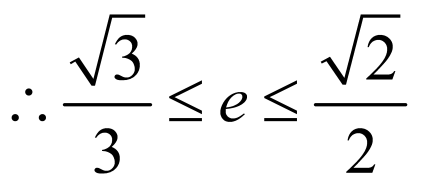 .故选:A
.故选:A
直线 与抛物线
与抛物线 方程联立得:
方程联立得: ,
,
因为直线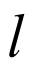 与抛物线
与抛物线 相交于A,B两点,所以
相交于A,B两点,所以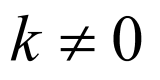 ,设
,设 ,
,
因此有 ,且
,且 ,
,
由 ,代入
,代入 中得:
中得:
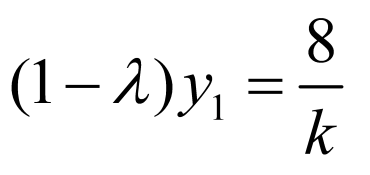 且
且 ,解得:
,解得: ,
,
函数 在
在 时单调递减,所以
时单调递减,所以 ,因此
,因此 ,
,
所以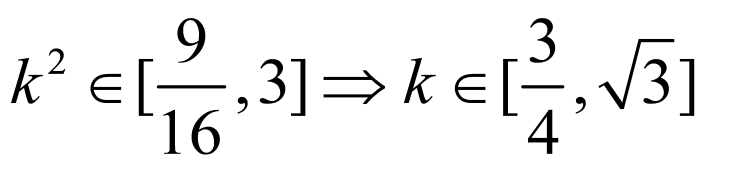 或
或 故选:C
故选:C
1.
因为直线 被圆
被圆 截得的弦长为
截得的弦长为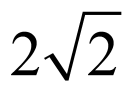 ,所以圆心到直线的距离为
,所以圆心到直线的距离为 ,即
,即 ,解得
,解得 或
或 .故选:AD.
.故选:AD.
对于A选项,由题意可得 ,故
,故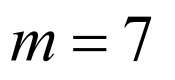 ,A错;
,A错;
对于B选项,对于双曲线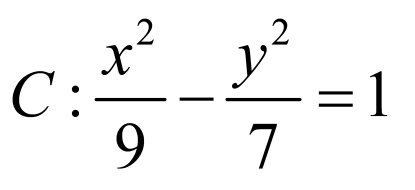 ,
, ,
, ,该双曲线的渐近线方程为
,该双曲线的渐近线方程为 ,B对;
,B对;
对于C选项, 的最小值为
的最小值为 ,C对;
,C对;
对于D选项,双曲线 的右焦点
的右焦点 到渐近线
到渐近线 的距离为
的距离为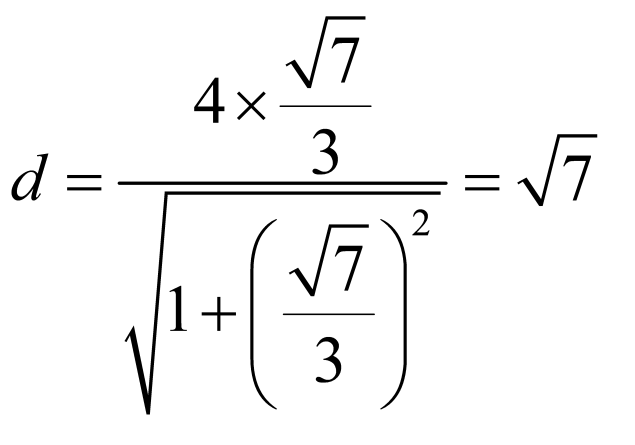 ,D对.故选:BCD.
,D对.故选:BCD.
由题意可得 ,设
,设 ,
, ,且
,且 ,
, ,
, ,
,
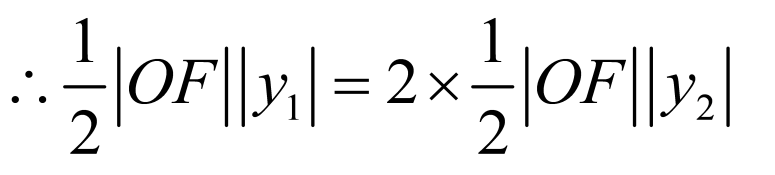 ,即
,即 ,联立
,联立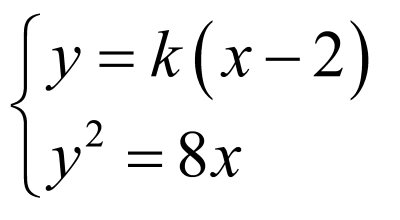 ,整理可得
,整理可得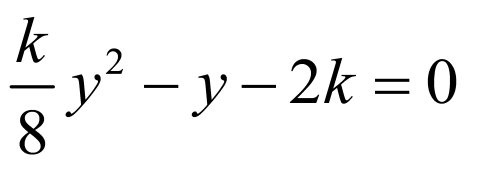 ,
,
 ,
, ,
, ,解得
,解得 ,
, ,
,
 ,解得
,解得 ,即
,即 ,
,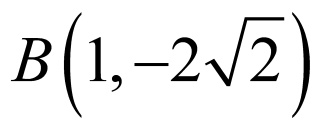 ,
,
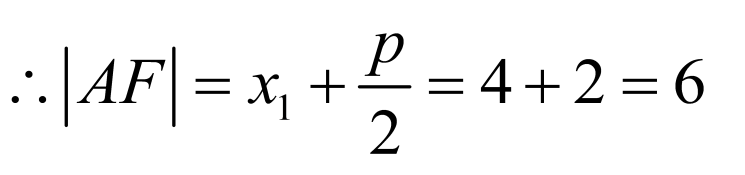 ,故A正确;
,故A正确;
 ,
, ,故B错误;
,故B错误;
线段 的中点为
的中点为 ,直径
,直径 ,
, 半径为
半径为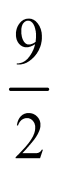 ,圆为
,圆为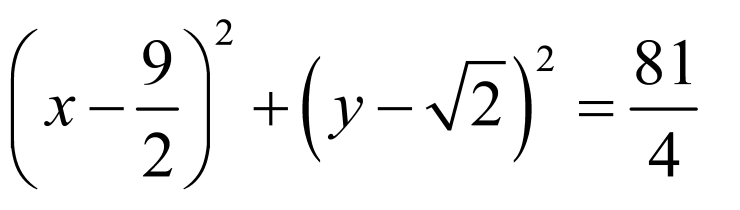 ,
,
所以 ,故C正确;
,故C正确;
 ,
, ,故D正确.故选:ACD
,故D正确.故选:ACD
由圆的方程可得: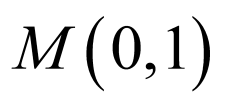 ,
, ,由椭圆的方程可得:椭圆的焦点恰好为
,由椭圆的方程可得:椭圆的焦点恰好为 ,
, ,
,
可得 ,
,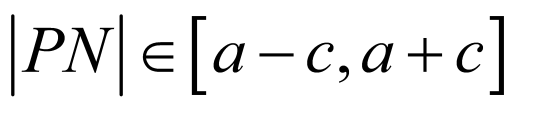 ,
,
所以 ,
, ,
, ,
,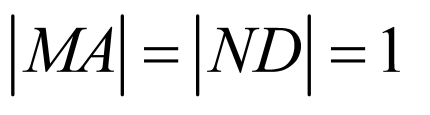 ,
,


 ,
,
设 ,
, ,令
,令 ,则
,则
在(1,2)上单减,在(2,3)上单增,所以当t=2时,即 时,
时,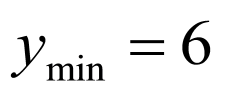 ,
,
当 或
或 时,即
时,即 或
或 时,
时, ,所以
,所以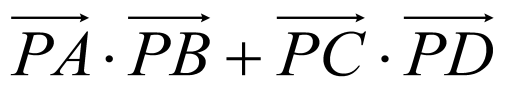 的取值范围是
的取值范围是
故选:BCD
填空题1.
设点 、
、 ,直线
,直线 的方程为
的方程为 ,即
,即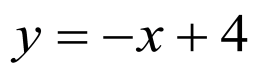 ,
,
联立 ,消去
,消去 可得
可得 ,解得
,解得 ,
, ,
,
因此, .故答案为:
.故答案为: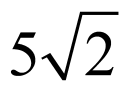 .
.
 ,显然半径为2,
,显然半径为2, ,由圆的性质可知:
,由圆的性质可知: ,
, 最大时,
最大时, 也就最大,显然
也就最大,显然 是锐角,因此
是锐角,因此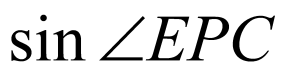 最大,
最大,
 ,要想
,要想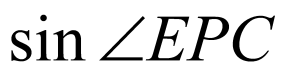 最大,只需
最大,只需 最小,当
最小,当 与直线
与直线 垂直时,因为
垂直时,因为 的斜率为1,所以
的斜率为1,所以 的斜率为
的斜率为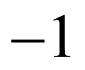 ,因此
,因此 的方程为:
的方程为: ,因此
,因此 ,所以此时
,所以此时 的坐标为:
的坐标为: ,故答案为:
,故答案为:

因为抛物线C的方程为 ,所以焦点
,所以焦点 ,根据题意直线l的方程为
,根据题意直线l的方程为 ,
,
设 ,联立
,联立 ,得
,得 ,所以
,所以 ,所以
,所以 ,
,
所以 ,因为AB的中点Q到x轴的距离为3,所以
,因为AB的中点Q到x轴的距离为3,所以 ,解得
,解得 ,
,
所以直线l的方程为 ,设点
,设点 关于直线l的对称点为
关于直线l的对称点为 ,所以
,所以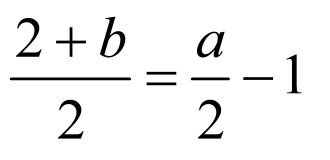 ,且
,且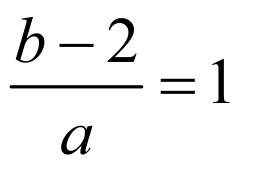 ,
,
解得 ,所以点F关于直线l的对称点为
,所以点F关于直线l的对称点为 ,
,
所以 ,当M在射线
,当M在射线 与直线l的交点时,取等号,故答案为:1.
与直线l的交点时,取等号,故答案为:1.
解:双曲线 ,且
,且 的渐近线方程为
的渐近线方程为 ,
, ,
,
令 ,可得
,可得 ,设
,设 ,可得
,可得 ,
, ,
,
则 ,
,
可得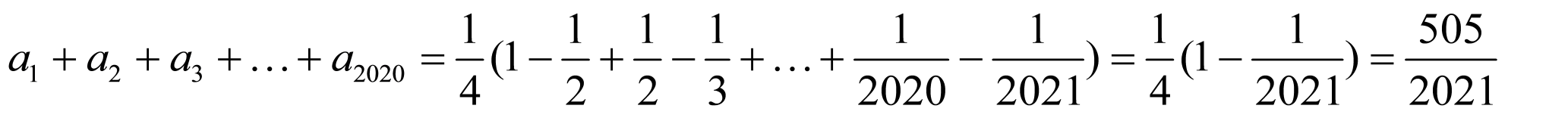 .
.
故答案为: ;
; .
.
1.
解:由题意设双曲线 的标准方程为
的标准方程为 ,
,
因为双曲线 与椭圆
与椭圆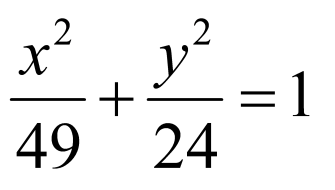 有公共焦点,所以
有公共焦点,所以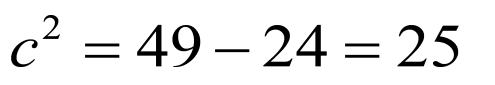 ,所以
,所以 ,
,
若选①,因为虚轴长是实轴长两倍,所以 ,即
,即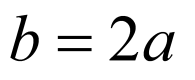 ,
,
因为 ,所以
,所以 ,得
,得 ,所以
,所以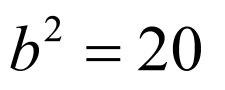 ,
,
所以双曲线 的标准方程为
的标准方程为 ;
;
若选②,因为离心率 ,所以
,所以 ,由
,由 ,得
,得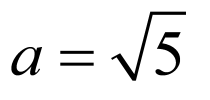 ,
,
所以 ,所以双曲线
,所以双曲线 的标准方程为
的标准方程为
(1)设 ,
,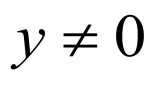 即
即 ,又
,又 ,则
,则 ,
,
∵A在圆x2+y2=25上,∴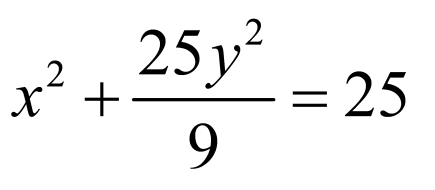 ,标准方程为
,标准方程为 .
.
(2)由(1)知:轨迹为焦点在x轴上的椭圆去掉左右顶点,而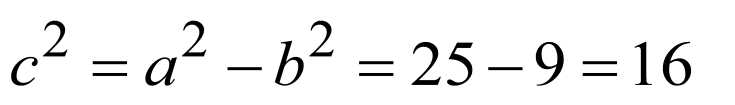 ,
,
∴焦点为 .
.
解:(Ⅰ) ,即
,即 ,
, ,准线
,准线 ,
,
设⊙C的方程为 ,将O、F、A三点坐标代入得:
,将O、F、A三点坐标代入得:
 ,解得
,解得 ∴⊙C的方程为
∴⊙C的方程为
(Ⅱ)设点B坐标为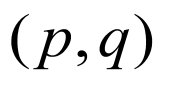 ,则
,则 ,整理得:
,整理得:
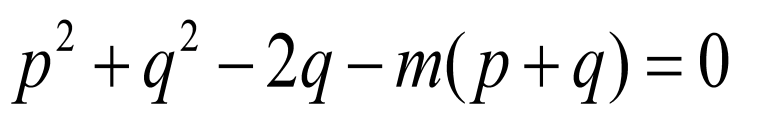 对任意实数
对任意实数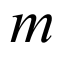 都成立 ∴
都成立 ∴ ,解得
,解得 或
或 ,
,
故当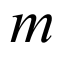 变化时,⊙C经过除原点O外的另外一个定点B
变化时,⊙C经过除原点O外的另外一个定点B
(Ⅲ)由B 、
、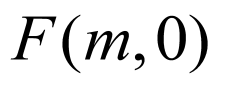 、
、 得
得 ,
,
∴ ,解得
,解得 又
又 ,∴
,∴
又椭圆的离心率 (
( )∴椭圆的离心率的范围是
)∴椭圆的离心率的范围是
(1)设椭圆E的半焦距为c,
则 ,解得
,解得 ,所以椭圆方程为
,所以椭圆方程为 ;
;
(2)由(1)得 ,
,
若 ,则
,则 ,代入椭圆方程得
,代入椭圆方程得 ,得
,得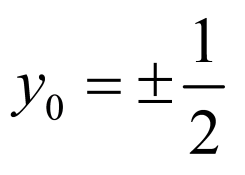 ;
;
若 ,则
,则 ,代入椭圆方程得
,代入椭圆方程得 ,得
,得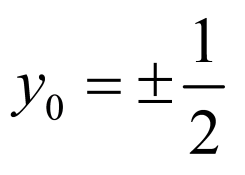 ;
;
若 ,则
,则 ,又
,又 ,解得
,解得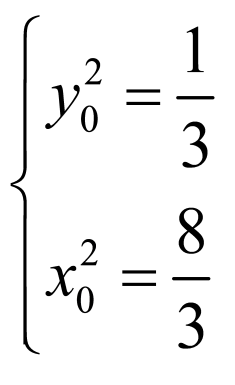 ,所以
,所以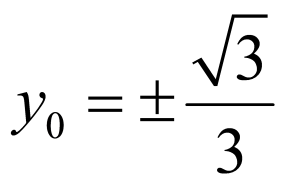
综上,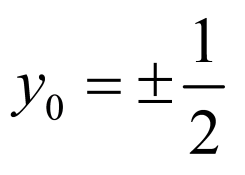 或
或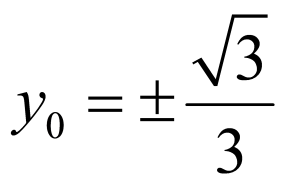 满足题意.
满足题意.
(1)∵抛物线 :
: 的焦点
的焦点 到其准线的距离为
到其准线的距离为 ,即
,即 ,
,
∴抛物线 的方程为
的方程为 .焦点坐标为
.焦点坐标为 ;
;
(2)过焦点 且倾斜角为
且倾斜角为 的直线
的直线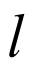 的方程为
的方程为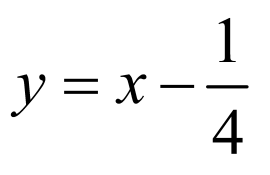 ,
,
联立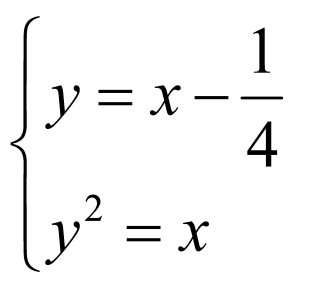 ,得
,得 .设
.设 ,
, ,
,
则 ,∴
,∴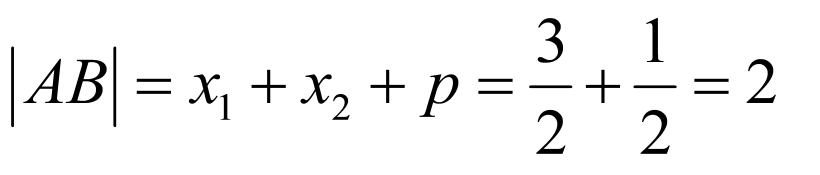 .
.
(1)由题意,令 ,则
,则 ,所以
,所以 ,即
,即 ,又因为
,又因为 的周长等于8,即
的周长等于8,即 ,则
,则 ,所以
,所以 ,故C的标准方程为
,故C的标准方程为 ;
;
(2)联立 ,消去
,消去 得
得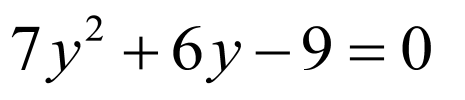 ,设
,设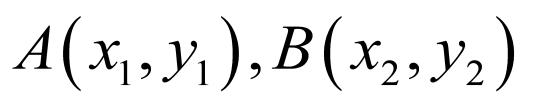 ,结合韦达定理
,结合韦达定理 ,则
,则 ,
,
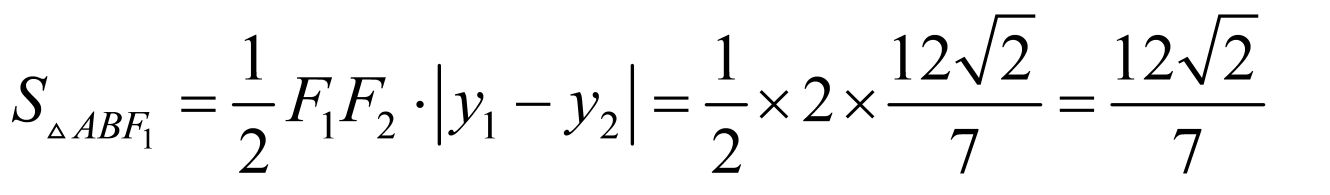 .
.
第五张
单选题
1. A
2. C
3. C
4. C
5. A
6. D
7. A
8. A
多选题
1. B,C
2. A,C
3. B,C
4.B,C
填空题
1.
解:设 ,
, ,
,
由双曲线的定义可知 ,
,
在△ 中,由余弦定理可得
中,由余弦定理可得 ,
,
 ,
,
 ,即
,即 ,
,

 ,
,
故答案为: .
.
解:由 ,所以有
,所以有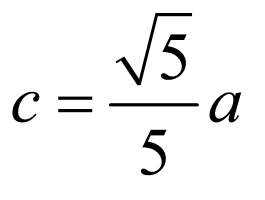 ,又
,又 ,所以
,所以 ,
,
又 在椭圆上,记左焦点为
在椭圆上,记左焦点为 ,则
,则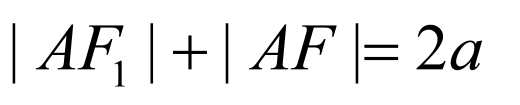 ,
,
所以 ,
,
当 时,
时, 有最小值,
有最小值,
即点 到直线
到直线 的距离
的距离 ,
,
所以 ,
,
故答案为: .
.
解: 为圆
为圆 上任意一点,
上任意一点,
则 到直线
到直线 的距离
的距离 ,即
,即 ,
,
则 ,
,
设圆 与直线
与直线 相切,则
相切,则 ,解得
,解得 .
.
 的最小值为
的最小值为 ,最大值为
,最大值为 ,
,
 ,则
,则 ,
,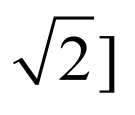 ,
,
故答案为: ,
,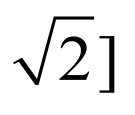 .
.

解:如图所示,设椭圆的长半轴长为 ,
,
双曲线的实半轴长为 ,焦距为
,焦距为 ,
,
由题意可知: ,
,
又 ,
,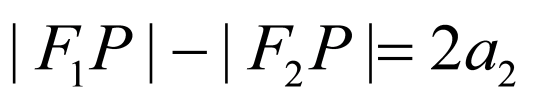 ,
,
 ,
, ,
,
两式相减,可得: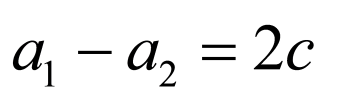 ,
,

 ,
,

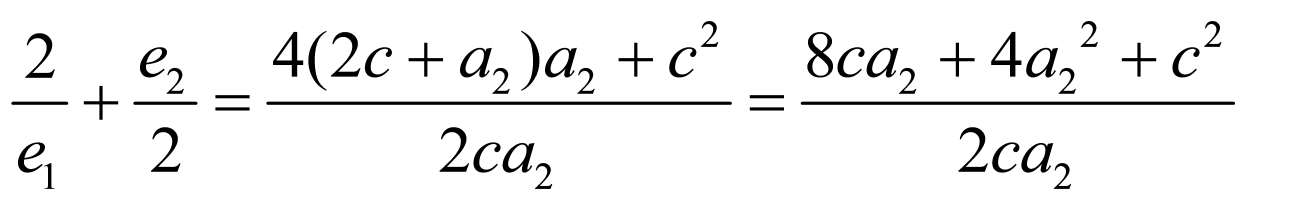
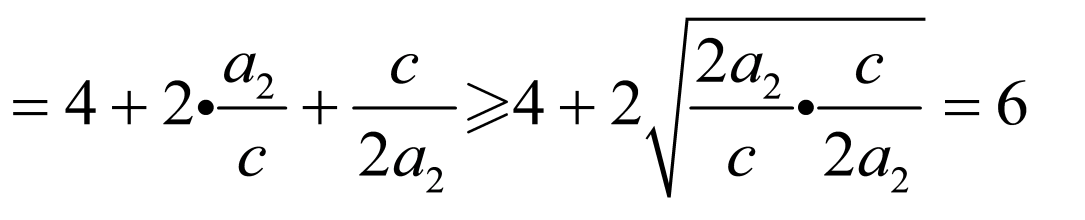 ,当且仅当
,当且仅当 时等号成立,
时等号成立,
则 的最小值为6,
的最小值为6,
故答案为:6.
1.
解:(1)由题意可知:点 ,
, ,
,
 的面积为3,
的面积为3,
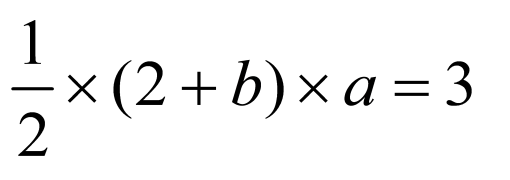 ,
,
又
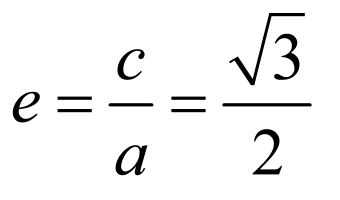 ,
, ,
,

 ,解得
,解得 ,
, ,
,
 椭圆
椭圆 的方程为:
的方程为: ;
;
(2)由题意可知,直线 的斜率存在,故设直线
的斜率存在,故设直线 的方程为
的方程为 ,点
,点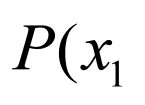 ,
, ,
, ,
,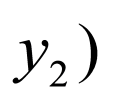 ,
,
则直线 的方程为
的方程为 ,令
,令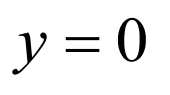 ,得点
,得点 的横坐标
的横坐标 ,
,
直线 的方程为
的方程为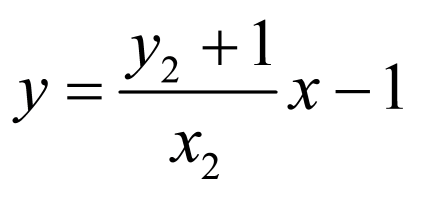 ,令
,令 ,得点
,得点 的横坐标
的横坐标 ,
,

 ,
,
把直线 代入椭圆
代入椭圆 得:
得: ,
,

 ,
,

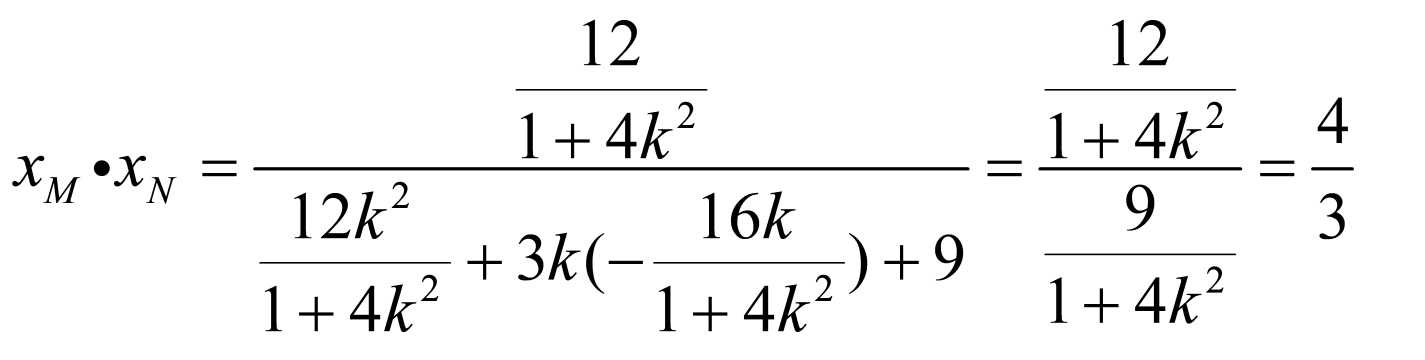 ,
,
(1)解:由题意可知, ,
,
所以曲线 是以
是以 ,
, 为焦点,长轴长为4的椭圆(除去与
为焦点,长轴长为4的椭圆(除去与 轴的交点),
轴的交点),
设曲线 ,
,
则 ,
, ,
,
解得 ,
, ,
,
所以曲线 的方程为
的方程为 ;
;
(2)①证明:设直线 的方程为
的方程为 ,
, ,
, ,
, ,
, ,
, ,
,
联立方程组 ,可得
,可得 ,
,
则 ,
,
因此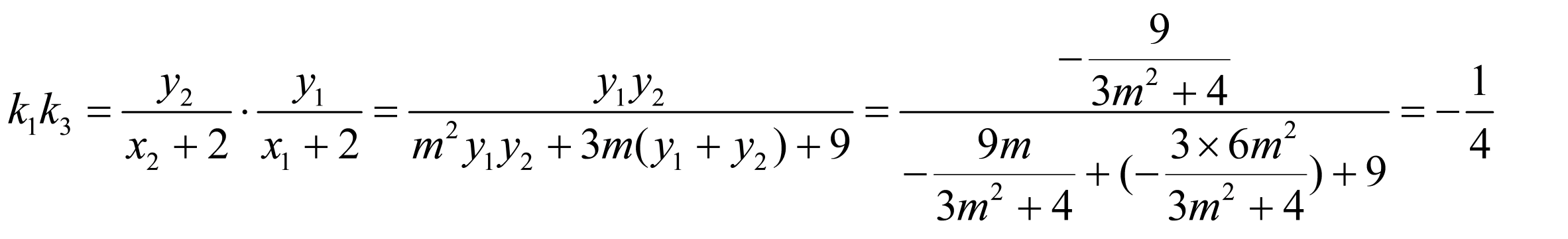 ,
,
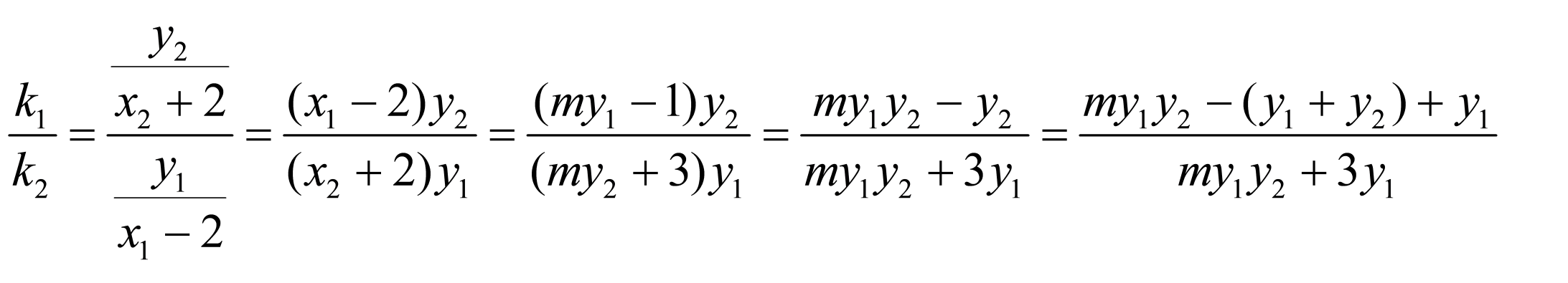 ,
,
故 ;
;
②解:由题意点 的坐标为
的坐标为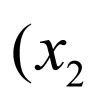 ,
, ,
,
则直线 的方程为
的方程为 ,
,
令 ,可得
,可得

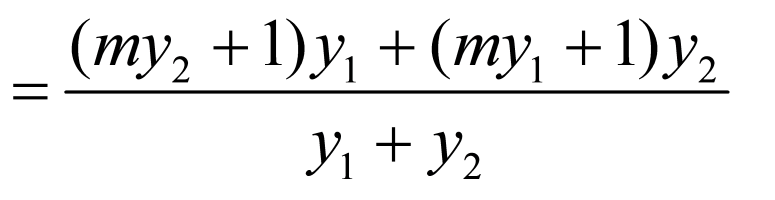

 ,
,
故直线 恒过点
恒过点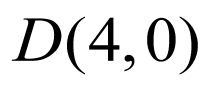 ,
,
所以


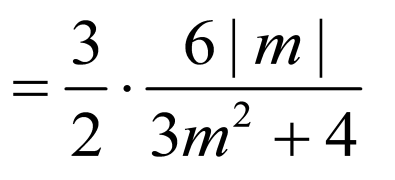
 ,
,
当且仅当 ,即
,即 时取等号,
时取等号,
此时 面积的最大值为
面积的最大值为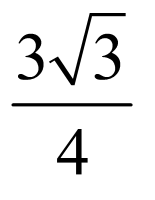 .
.
解:(1)由题意,设椭圆的方程为 ,
,
则 ,
,
 ,
,
所以 ,
, ,
,
所以椭圆 的标准方程为
的标准方程为 ,
,
(2)设 的平分线所在直线
的平分线所在直线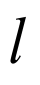 与
与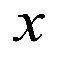 轴相交于点
轴相交于点 ,
,
因为 ,
, ,
,
因为 是角平分线,
是角平分线,
所以 ,
,
即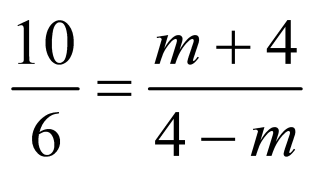 ,
,
解得 ,
,
所以角平分线 所在直线的斜率为
所在直线的斜率为 ,
,
所以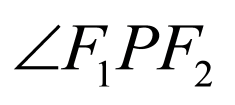 的平分线所在直线的方程为
的平分线所在直线的方程为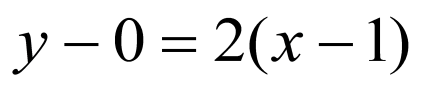 ,
,
即 .
.
解:(1)由离心率为 ,且
,且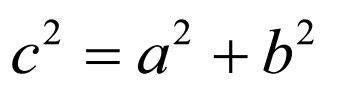 ,得
,得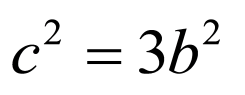 ,
, ,
,
即双曲线方程为 .
.
又点 在双曲线
在双曲线 上,
上,
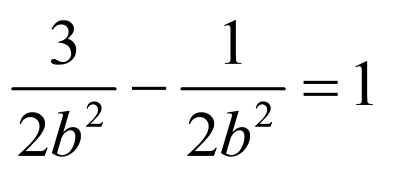 ,
,
解得 ,
, ,
,
 双曲线
双曲线 的方程为
的方程为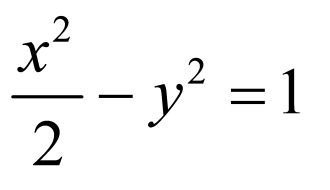 ;
;
(2)当直线 的斜率不存在时,点
的斜率不存在时,点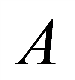 ,
, 关于
关于 轴对称,
轴对称,
设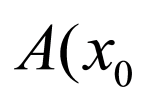 ,
, ,
, ,
,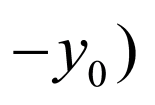 ,
,
则由 ,得
,得 ,
,
即 ,解得
,解得 ,不符合题意,故直线
,不符合题意,故直线 的斜率存在.
的斜率存在.
不妨设直线 的方程为
的方程为 ,代入
,代入 ,
,
整理得 ,△
,△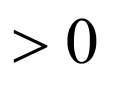 .
.
设 ,
, ,
, ,
,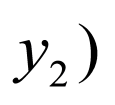 ,则
,则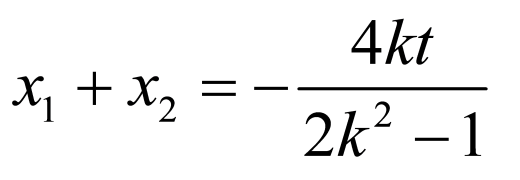 ,
,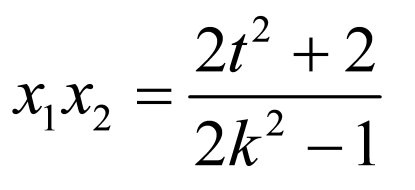
由 ,得
,得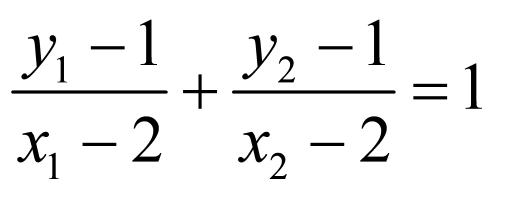 ,即
,即 ,
,
整理得 ,
,

 ,
,
整理得: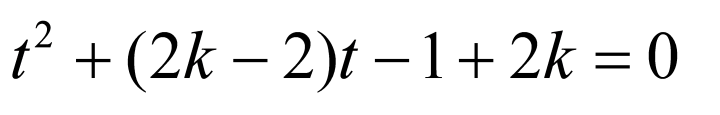 ,即
,即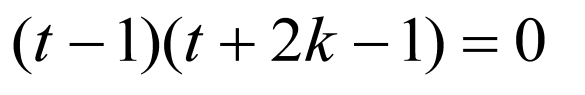 ,
,
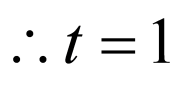 或
或 .
.
当 时,直线
时,直线 的方程为
的方程为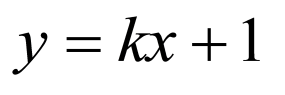 ,经过定点
,经过定点 ;
;
当 时,直线
时,直线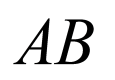 的方程为
的方程为 ,经过定点
,经过定点 ,不符合题意.
,不符合题意.
综上,直线 过定点
过定点 .
.
解:(1)由题意可知,点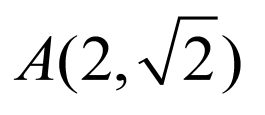 为椭圆与抛物线的交点,
为椭圆与抛物线的交点,
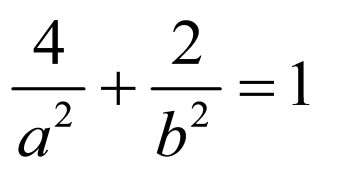 且
且 ,
,
解得 ,则
,则 ;
;
又直线 将△
将△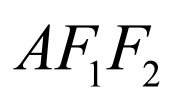 的面积分为
的面积分为 两部分,
两部分,
所以 ,解得
,解得 ,
,
则 ,解得
,解得 ,
,
抛物线的方程为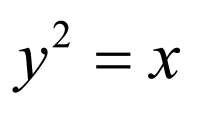 ;椭圆的方程为
;椭圆的方程为 ;
;
(2)设 ,
, ,
,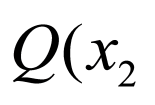 ,
,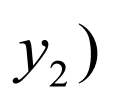 ,
,
由 ,可得
,可得 ,
,
由△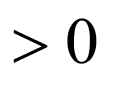 ,可得
,可得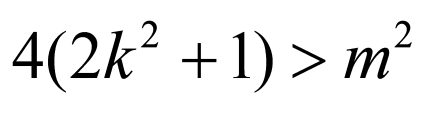 (※),
(※),
且 ,
,
由 重心恰好在圆
重心恰好在圆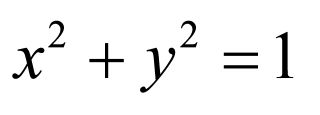 上,
上,
可得 ,
,
即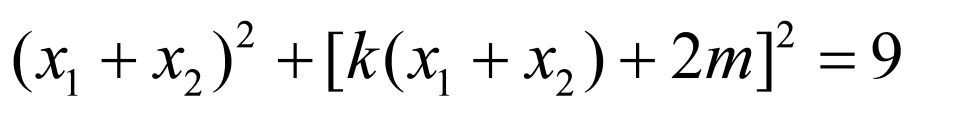 ,
,
即 ,
,
所以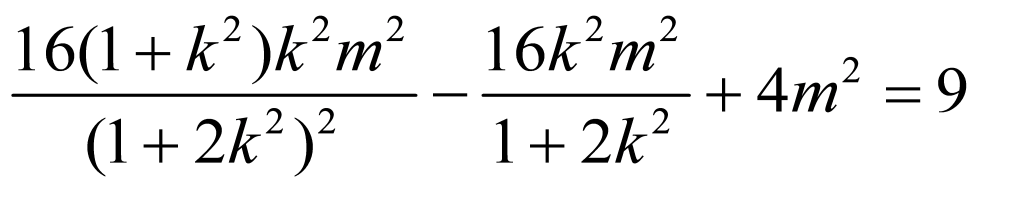 ,
,
化简得 ,代入(※)中可得
,代入(※)中可得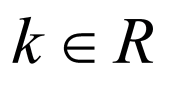 ,
,
设 ,
,
则 ,
,
当且仅当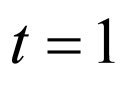 时取等号,
时取等号,
故 ,
,
则实数 的取值范围为
的取值范围为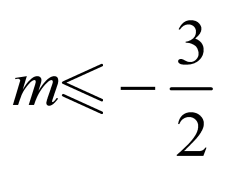 或
或 .
.
解:(1)设点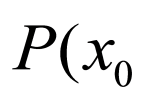 ,
,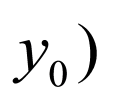 ,由椭圆的对称性可知点
,由椭圆的对称性可知点 ,
,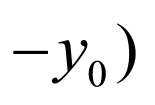 ,
,
不妨令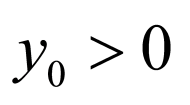 ,由题意可知
,由题意可知 ,
,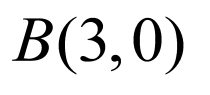 ,
,
所以 ,
,
由题意可知, ,
,
所以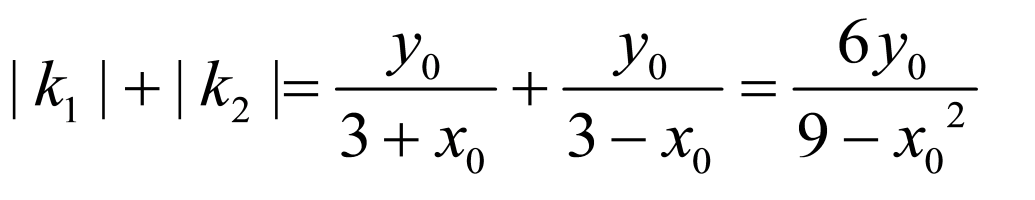 ,
,
由点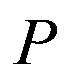 在椭圆上,则
在椭圆上,则 ,
,
则 ,
,
所以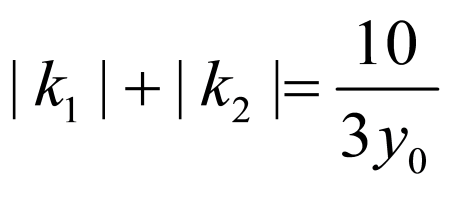 ,
,
因为 ,
,
所以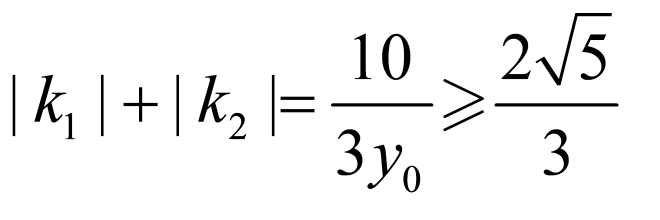 ,
,
当且仅当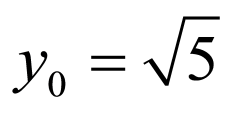 时等号成立,即
时等号成立,即 的最小值为
的最小值为 ;
;
(2)当直线 的倾斜角
的倾斜角 为锐角时,设
为锐角时,设 ,
,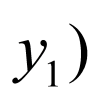 ,
,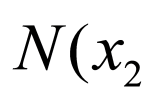 ,
, ,
,
设直线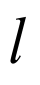 的方程为
的方程为 ,
,
联立方程组 ,可得
,可得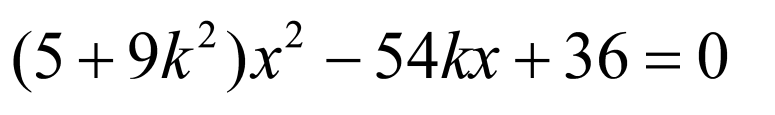 ,
,
从而△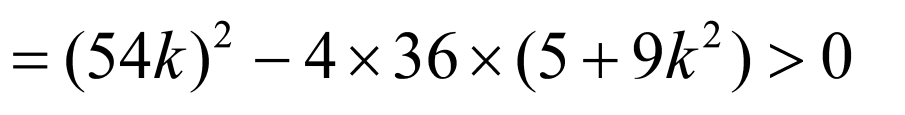 ,又
,又 ,解得
,解得 ,
,
所以 ,
,
又直线 的方程是
的方程是 ,
,
令 ,解得
,解得 ,所以点
,所以点 为
为 ;
;
直线 的方程是
的方程是 ,同理点
,同理点 为
为 ,
,
所以 ,
, ,
, ,
,
因为记 ,
,
所以 ,
,
所以




 ,
,
因为 ,所以
,所以 ,
,
综上所述,所以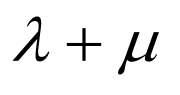 的范围是
的范围是 .
.
第六张
单选题
1. C
2. C
3. B
4.
 ,
,
 ,
,
 取得最大值时,
取得最大值时, 的值为7或8.
的值为7或8.
因为 ,
,
所以 时,
时, ,
,
两式相减得 ,
, ,
,
又 ,满足此式,所以
,满足此式,所以 ,
,
 ,
,
所以数列 的前10项和为
的前10项和为 .
.
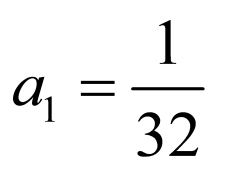 ,
, ,
,
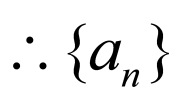 的前
的前 项和为
项和为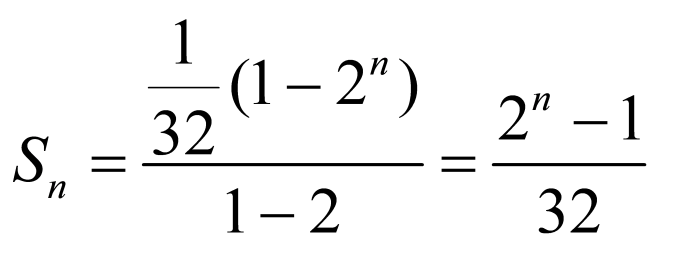 ,
,
 的前
的前 项积为
项积为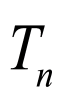 ,则
,则 ,
,
 ,
,
 ,即
,即 ,即
,即 ,
,
解得 ,
,
 ,则
,则 ,
,
因此满足条件的正整数 的最大值为12.
的最大值为12.
8.
由题意得 ,
,
所以 ,故数列
,故数列 为等比数列,但不一定为等差,
为等比数列,但不一定为等差, 错误;
错误;
当 时,
时, 没有意义,
没有意义, 错误;
错误;
 有可能为0,
有可能为0, 错误;
错误;
若 ,则
,则 ,
, 时,
时, ,
,
由数列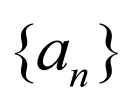 为等比数列得,
为等比数列得, ,
,
所以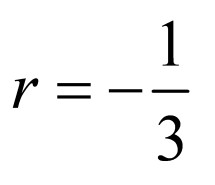 ,
, 正确.
正确.
1.
q= 或q=﹣1(舍),
或q=﹣1(舍),
所以数列{an|为单调递减数列,A错误,B正确;
因为an=20×( )n﹣1,易得a5>1,a6<1,
)n﹣1,易得a5>1,a6<1,
所以Tn的最大值为T5,C正确,D错误.
2.
由{an}是等差数列,且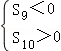 ,得
,得 ,
,
所以|a6|>|a5|,即a5是数列{an}中绝对值最小的项,选项A错误;
由题意,S3,S6﹣S3,S9﹣S6,S12﹣S9构成等差数列,
令S3=k,根据 =
= ,得S6=4k,则k,3k,S9﹣4k,S12﹣S9构成等差数列,
,得S6=4k,则k,3k,S9﹣4k,S12﹣S9构成等差数列,
所以 ,解得
,解得 ,
,
所以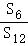 =
=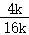 =
= ,选项B错误;
,选项B错误;
若a1=8,a4=2,则3d=a4﹣a1=﹣6,即d=﹣2,
所以an=8﹣2(n﹣1)=﹣2n+10,故|a1|+|a2|+⋯+|a8|=8+6+4+2+0+2+4+6=32,选项C正确;
由{an}是等差数列,|a4|=|a8|,d≠0,得a4=﹣a8,则a4+a8=0,
所以S11=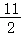 (a1+a11)=
(a1+a11)= (a4+a8)=0,选项D正确.
(a4+a8)=0,选项D正确.
A选项:
 ,故A正确;
,故A正确;
B选项: ,故B正确;
,故B正确;
D选项: ,故D错误;
,故D错误;
C选项: ,故C正确.
,故C正确.
解: ,
, ,即
,即 ,
,
又 ,
,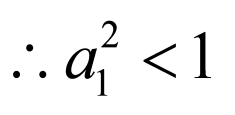 且
且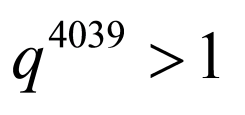 ,
,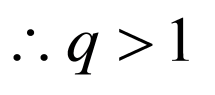 ,等比数列
,等比数列 是一个增数列,
是一个增数列, 正确,
正确,
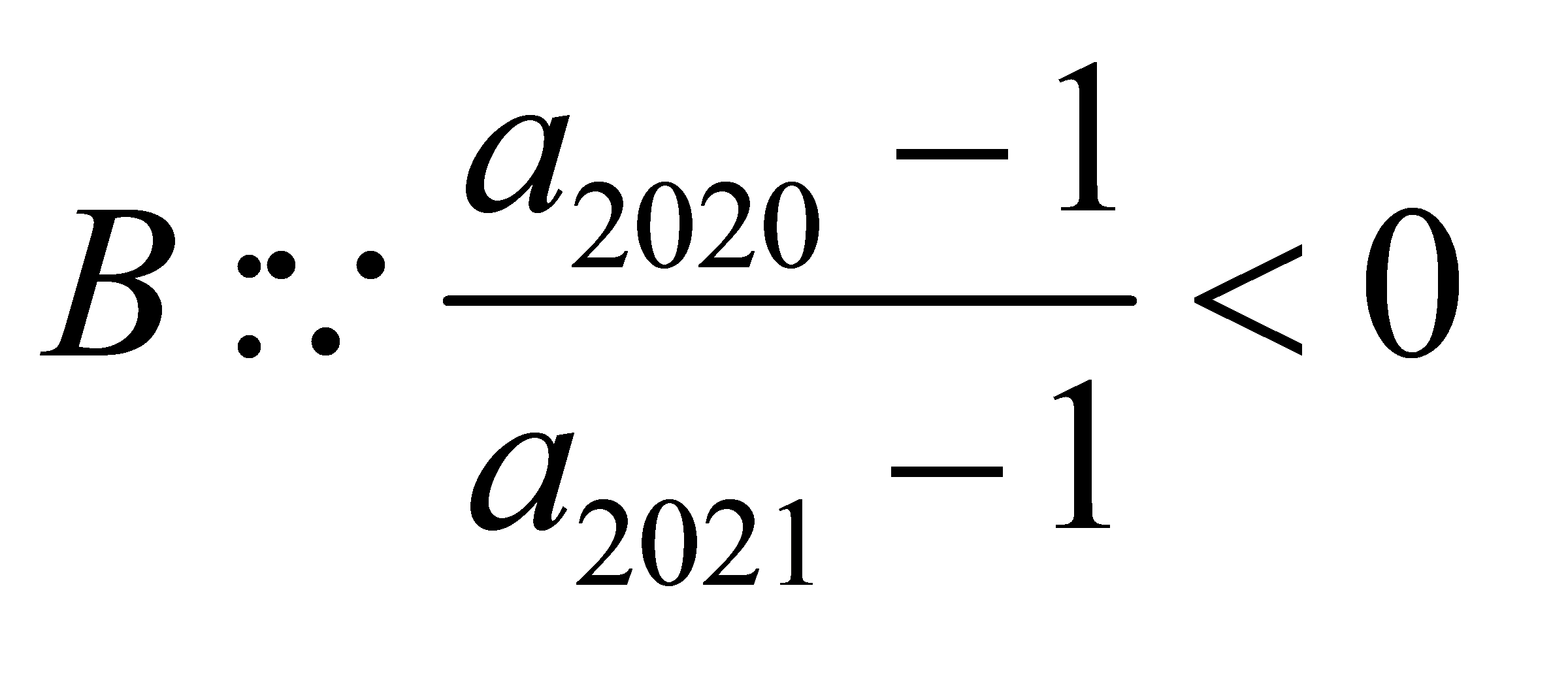 ,
, ,且
,且 ,
,
即 且
且 ,
,
 ,
,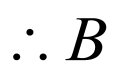 正确,
正确,
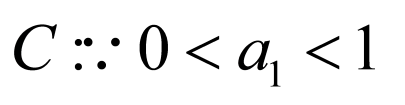 ,
,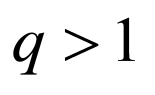 ,
, 等比数列
等比数列 是一个增数列,
是一个增数列,
又 且
且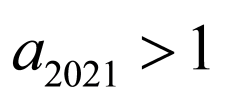 ,
,
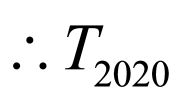 的值是
的值是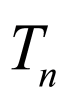 中最小的,
中最小的, 错误,
错误,
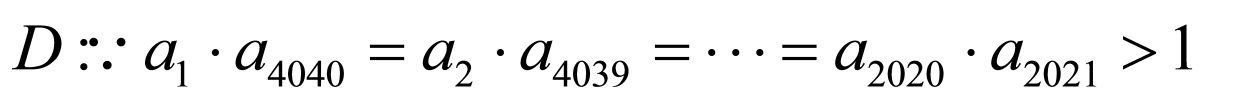 ,
,
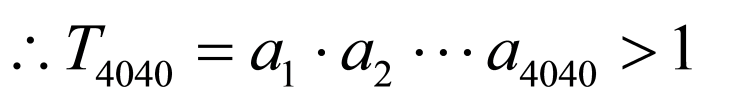 ,
,
 ,
, 使
使 成立的最大正整数
成立的最大正整数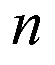 的值为4039,
的值为4039, 正确,
正确,
1.
设等比数列的公比为q,由a3+a15=12,
可得 +a9q6=12,则a9=
+a9q6=12,则a9=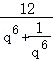 ,
,
由基本不等式得q6+ ≥2
≥2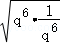 =2,
=2,
当且仅当q6= ,即q=±1时等号成立,
,即q=±1时等号成立,
所以q6+ 的最小值是2,所以当q=±1时,a9的最大值为6.
的最小值是2,所以当q=±1时,a9的最大值为6.
在数列{an}中,a1=1,且a1•a2•…•an=n2,•••①
可得a1•a2•…•an﹣1=(n﹣1)2(n≥2),•••②,
 可得n≥2时,an
可得n≥2时,an .
.
设等比数列 的公比为
的公比为 ,
,
当 时,
时, ,
,
当 时,
时, ,解得
,解得 ,
,
所以 ,
, ,
, ①,
①,
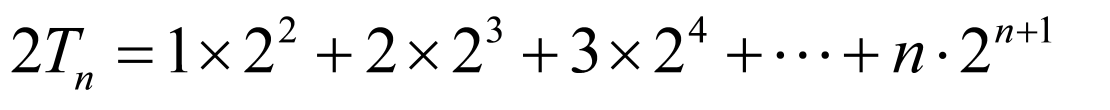 ②,
②,
由①-②得 ,
,
故答案为 .
.
因为等差数列 满足
满足 ,
, ,
,
所以 ,所以
,所以 ,
,
则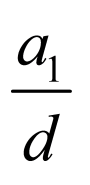 的取值范围是
的取值范围是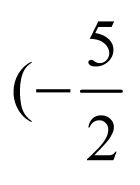 ,
, ;
;
 ,
,
由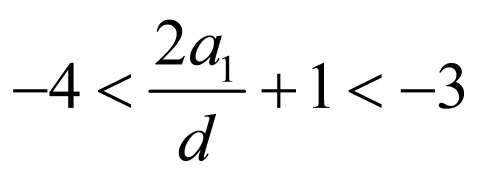 ,所以
,所以 ,
,
所以, 的取值范围是
的取值范围是 ,
, .
.
故答案为: ,
, ;
;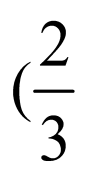 ,
, .
.
1.
解:(1)设 的公差为
的公差为 ,则
,则
解得 故
故 .
.
(2)由(1)可知, ,
,
由二次函数的性质知 单调递增,
单调递增,
因为 ,
, ,
,
所以当 时,
时, ,故
,故 的最小值为12.
的最小值为12.
解:(1)由题意 ,
,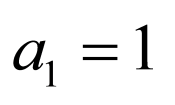 ,
,
所以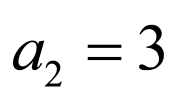 ,
, ,
, ;
;
(2)因为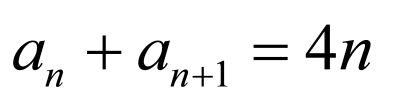 ,
,
所以 ,
,
两式相减得, ,
,
所以数列 是以4为公差,以3为首项的等差数列,
是以4为公差,以3为首项的等差数列,
所以 .
.
解:(1)由 是等差数列,得
是等差数列,得 ,即
,即 ,解得
,解得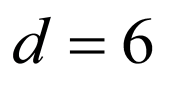 ,
,
又 ,得
,得 ,解得
,解得 ,
,
所以数列 的公差
的公差 和
和 分别为6,
分别为6, ;
;
(2)由(1)可知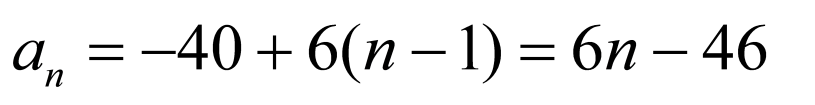 ,令
,令 ,
,
得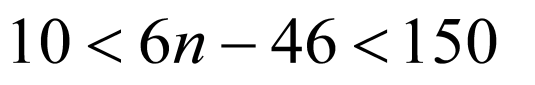 ,解得
,解得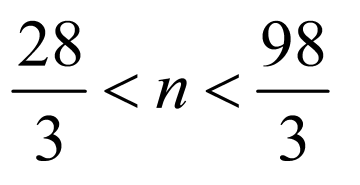 ,又
,又 ,所以
,所以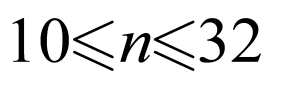 ,
,
因此满足 的共有23项.
的共有23项.
(1)因为 ,
, ,
, ,
,
所以 ,即
,即 ,
,
所以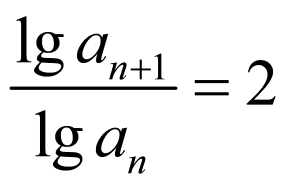 ,
,
因为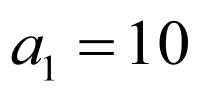 ,所以
,所以 ,
,
所以数列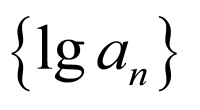 是以1为首项,2为公比的等比数列,
是以1为首项,2为公比的等比数列,
所以 ,所以
,所以
(2)由(1)可知 ,
,
所以数列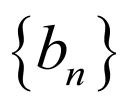 的前n项积
的前n项积 为
为

 ,
,
令 ,
,
则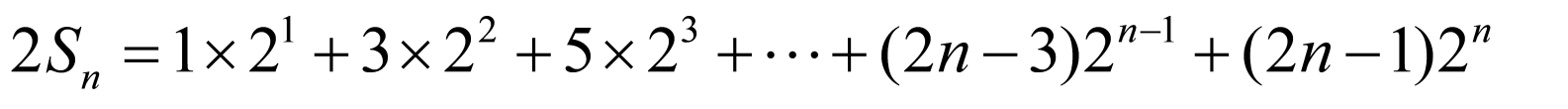 ,
,
所以


 ,
,
所以 ,
,
所以
设等差数列 的公差为
的公差为 .
.
(1)选①②,证明③成立.
若 ,则
,则 ,解得
,解得 ,
,
所以 ,则
,则 ,
,
所以
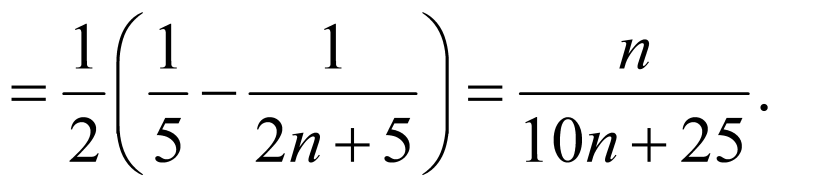 故选择①②为条件,则③成立.
故选择①②为条件,则③成立.
(2)选①③,证明②成立.
若 ,则
,则 ,与③相互矛盾,故
,与③相互矛盾,故 ,则
,则 ,
,
所以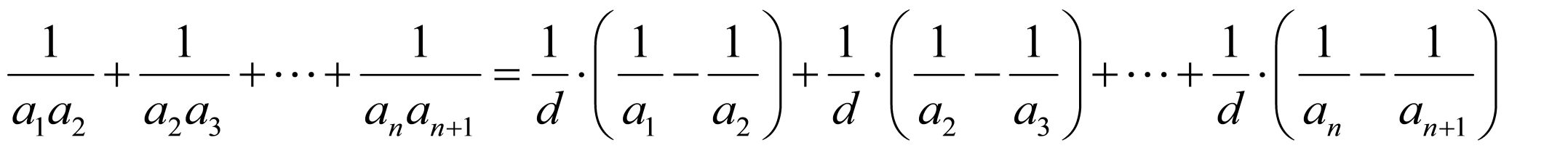
 ,
,
故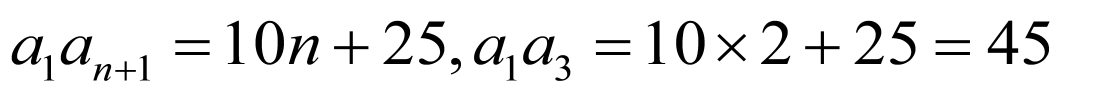 ,解得
,解得 ,
,
所以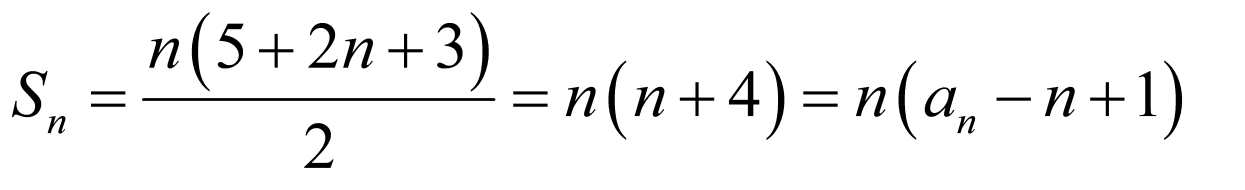 ,故选择①③为条件,则②成立.
,故选择①③为条件,则②成立.
(3)选②③,证明①成立.
若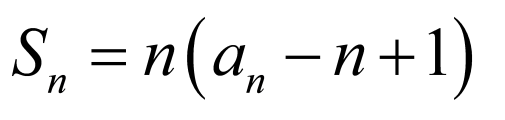 ,则
,则 ,解得
,解得 ,
,
所以 ,
,
所以
 ,
,
所以 ,且
,且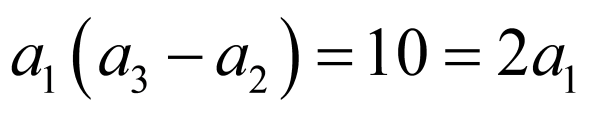 ,解得
,解得 ,故选择②③为条件,则①成立.
,故选择②③为条件,则①成立.
(1)证明:由已知可得: ,
,


 ,
,
 是公差为1的等差数列;
是公差为1的等差数列;
(2)解:由(1)可得 ,
,
 ,
,
结合图象易知函数 在
在 ,
,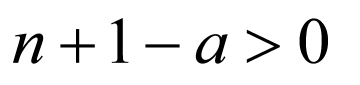 时取到最小值,
时取到最小值,
 由
由 为数列
为数列 中的最小项,有
中的最小项,有 ,
,
解得: ,
,
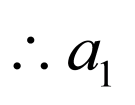 的取值范围是:
的取值范围是: .
.
第七张
单选题
1
C
2由
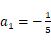 ,排除A,C;由
,排除A,C;由  ,排除B.
,排除B.
因为
 ,
,
所以由
 ,得
,得  ,
,
则  ,
, ,
, ,
, .
.
累加得: .
.
当  ,
, 符合上式,
符合上式,
所以  .
.
则  .
.
所以

由题意得, .
.
由题意,此数列分子和分母之和为
 的有一个,为
的有一个,为  的有
的有 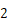 个,为
个,为 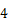 的有
的有  个,
个,
按此规律,知
 出现在和为
出现在和为  的那一组中,
的那一组中,
又每一组的数都是以分子为
 开始的,故
开始的,故  是分子分母和为
是分子分母和为  那一组的第
那一组的第  个数,
个数,
由于  为
为  的第第
的第第  组,前
组,前 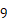 组共有
组共有  个数,
个数,
故  是第
是第  个数,即第
个数,即第  项.
项.
数列
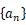 的各项值为
的各项值为  ,
, ,
,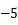 ,
, ,
, ,
, ,
,
所以各项绝对值构成一个以
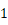 为首项,以
为首项,以  为公差的等差数列,
为公差的等差数列,
所以 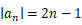 ,又因为数列的奇数项为负,偶数项为正,
,又因为数列的奇数项为负,偶数项为正,
所以 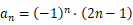 .
.
因为
 ,
,
所以  令
令
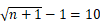 ,得
,得  .
.
由题意,

1
 .
.
当  时可得,
时可得,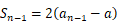 ,
,
两式相减可得, ,
, ,
,
又  时,
时,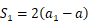 可得,
可得, ,
,
若  时,数列
时,数列  不是等比数列,而是等差数列,其各项都为
不是等比数列,而是等差数列,其各项都为
 ,和也为等差数列;
,和也为等差数列;
当  时,数列
时,数列  是等比数列,不是等差数列,而非常数性等比数列的前
是等比数列,不是等差数列,而非常数性等比数列的前
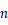 项和不是等比.
项和不是等比.
ACD
3设此人第
 天走
天走  里路,则数列
里路,则数列  是首项为
是首项为  ,公比为
,公比为  的等比数列,
的等比数列,
因为 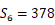 ,
,
所以  ,解得
,解得  ,
,
对于A,由于
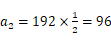 ,所以此人第二天走了九十六里路,所以A正确;
,所以此人第二天走了九十六里路,所以A正确;
对于B,由于
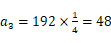 ,
, ,所以B不正确;
,所以B不正确;
对于C,由于
 ,
, ,所以此人第一天走的路程比后五天走的路程多六里,所以C正确;
,所以此人第一天走的路程比后五天走的路程多六里,所以C正确;
对于D,由于
 ,所以D正确.
,所以D正确.
根据题意,需要满足的条件应该为

即 
综上  .
.
 可能的范围应该为
可能的范围应该为  的子集,只有CD符合条件,
的子集,只有CD符合条件,
故选CD.
故选CD.
填空题1
因为
 ,即
,即  ,
,
所以 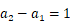 ,
, ,
, ,
, ,
, ,
,
将上述
 个式子相加得:
个式子相加得:

又因为
 ,所以
,所以 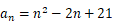 .
.
由数列
 的前
的前 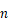 项和
项和 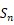 ,且满足
,且满足 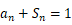 ,
,
当  时,
时, ,
,
两式相减,可得
 ,即
,即  ,
,
令  ,可得
,可得  ,解得
,解得  ,
,
所以数列
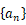 表示首项为
表示首项为  ,公比为
,公比为  的等比数列,
的等比数列,
所以  ,则
,则  ,
,
所以  ,
,
所以

故答案为: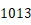 .
.
设第
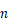 行,第
行,第  列为
列为 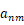 ,
,
则第  行第
行第  列为
列为 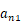 ,第
,第  行第一列为
行第一列为  ,
,
由题意知
 ,
,
所以  ,
,
所以  ,
, ,
,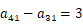 ,
, ,
, ,
,
所以  ,
,
因为  ,
,
所以  ,
,
由题意知
 ,
, ,
, ,
,
 ,
,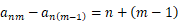 (
(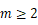 ),
),
所以 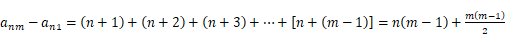 ,
,
所以  ,
,
所以第
 行第
行第 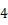 列为
列为  ,
,
所以第
 行,第
行,第 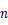 列为
列为  ,
,
故答案为
 ;
; .
.
当  时,
时,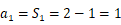 ;
;
当  时,
时, .
.
经检验,当
 时,
时, 满足上述式子,
满足上述式子,
故数列
 的通项公式
的通项公式 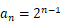 .
.
1
由
 得
得  ,
,
又因为
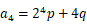 ,
, ,且
,且 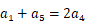 ,
,
 ,
,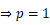 ,
, .
.
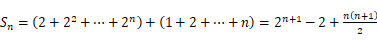 .
.
因为
 ,
,
所以当
 时,
时, ,
,
解得  ,
,
当 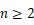 且
且 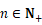 时,
时,
 ,
,
所以  ,
,
即  (
( 且
且  ),
),
经检验,
当  时,
时, 满足
满足  ,
,
所以 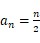 (
( ).
).
由( )知
)知  ,
,
所以

当  时,
时, ,解得:
,解得: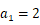 ;
;
当  时,
时, ,解得:
,解得: 或
或  (舍);
(舍);
当 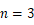 时,
时, ,解得:
,解得: 或
或  (舍).
(舍).
所以  ;
; ;
; .
.
由(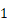 )知:
)知: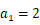 ,
,
当 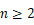 时,
时, ,
,
 ,
,
相减得: ,
,
整理得: ,
,
因为  是正数组成的数列,
是正数组成的数列,
所以 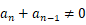 ,所以
,所以  ,
,
所以  为以
为以  为首项,
为首项, 为公差的等差数列,
为公差的等差数列, .
.
 ,
,

 随
随  的增大而增大,且恒小于
的增大而增大,且恒小于 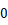 ,所以
,所以  ,
,
因为  对所有
对所有  都成立,所以
都成立,所以  即
即 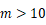 ,
,
故最小正整数
 的值为
的值为  .
.
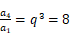 ,所以
,所以  ,
,
所以  ,
, ,
,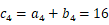 ,
, ,
,
所以 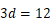 ,
, ,
,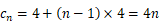 ,
,
所以  ,
, ,
,
即 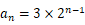 ,
, .
.

 是一具满足条件的
是一具满足条件的 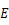 数列
数列  .
.
(答案不唯一, 也是一个满足条件的
也是一个满足条件的  的数列
的数列  ).
).
必要性:
因为  数列
数列  是递增数列,
是递增数列,
所以  (
( ).
).
所以  是首项为
是首项为  ,公差为
,公差为  的等差数列.
的等差数列.
所以  .
.
充分性,
由于

所以  ,即
,即  .
.
又因为
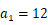 ,
, ,
,
所以  .
.
故  (
( ),即
),即  是递增数列.
是递增数列.
综上,结论得证.
令 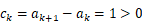 (
( ),则
),则  .
.
因为

所以

因为  ,
,
所以  为偶数(
为偶数( ).
).
所以  为偶数,
为偶数,
所以要使
 ,
,
必须使
 为偶数,
为偶数,
即 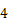 整除
整除 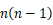 ,即
,即  或
或  (
( ),
),
当  (
( )时,
)时,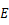 数列
数列  的项满足
的项满足 
( )时,有
)时,有  ,
, ;
;
 (
( ),
), 时,有
时,有  ,
, ;
;
当  (
( )时,
)时, 数列
数列  的项满足,
的项满足, ,
,
当 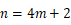 或
或 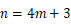 (
( )时,
)时, 不能被
不能被  整除,此时不存在
整除,此时不存在  数列
数列  ,
,
使得  ,
, .
.
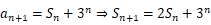 ,
,
 ,
, ,
,
当 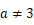 时,
时,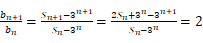 ,
,
所以  为等比数列.
为等比数列.
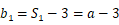 ,
, .
.
由( )可得
)可得 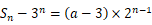 .
.
 ,
, ,
, ,
,
所以 
因为  ,
,
所以  ,又
,又  ,
,
所以  的最小值为
的最小值为  .
.
由( )当
)当  时,
时, ,
,
当  时,
时,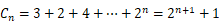 ,
, ,
,
所以对正整数
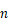 都有
都有  .
.
由  ,
, ,
,
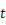 只能是不小于
只能是不小于  的奇数.
的奇数.
①当
 为偶数时,
为偶数时, ,
,
因为  和
和  都是大于
都是大于 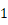 的正整数,
的正整数,
所以存在正整数
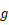 ,
, ,
,
使得  ,
, ,
, ,
, ,
,
所以
 且
且  ,
, ,
,
相应的
 ,即有
,即有  ,
,
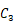 为“指数型和”;
为“指数型和”;
②当
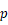 为奇数时,
为奇数时, ,
,
由于  是
是  个奇数之和,
个奇数之和,
仍为奇数,又
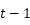 为正偶数,
为正偶数,
所以  不成立,此时没有“指数型和”.
不成立,此时没有“指数型和”.
第八张
根据 的元素判断两者间的包含关系.
的元素判断两者间的包含关系.
【详解】
依题意,集合 的元素是
的元素是 的倍数,集合
的倍数,集合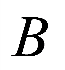 的元素是
的元素是 的倍数,所以集合
的倍数,所以集合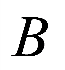 是集合
是集合 的真子集.
的真子集.
故选:D
根据曲线表示椭圆,可求得t的范围,根据充分、必要条件的定义,即可得答案.
【详解】
因为曲线 为椭圆,
为椭圆,
所以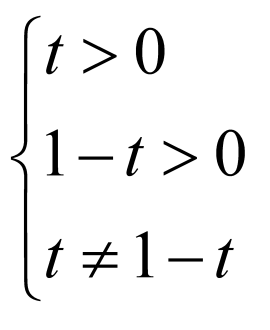 ,解得
,解得 且
且 ,
,
所以“ ”是“
”是“ 且
且 ”的必要而不充分条件.
”的必要而不充分条件.
故选:B
取 中点
中点 ,连接
,连接 、
、 ,∵
,∵ 、
、 分别为
分别为 、
、 中点,可得
中点,可得 ,
, ,从而得到
,从而得到 是
是 与
与 所成的角,即可得到答案.
所成的角,即可得到答案.
【详解】
解:取 中点
中点 ,连接
,连接 、
、 ,∵
,∵ 、
、 分别为
分别为 、
、 中点,
中点,

∴ ,且
,且 ,
, ,且
,且 ,
,
∵ ,
, ,∴
,∴ ,∵
,∵ ,
,
∴ 是
是 与
与 所成的角,
所成的角,
在 中,∵
中,∵ ,
, ,
, ,∴
,∴ ,
,
即 与
与 所成的角为
所成的角为 ,
,
故选:A.
设出对称点,根据对称 关系列出式子即可求解.
【详解】
解:设点 关于直线
关于直线 的对称点是
的对称点是 ,
,
则有 ,解得
,解得 ,
, ,
,
故点 关于直线
关于直线 的对称点是
的对称点是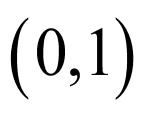 .
.
故选:B.
【点睛】
方法点睛:关于轴对称问题:
(1)点 关于直线
关于直线 的对称点
的对称点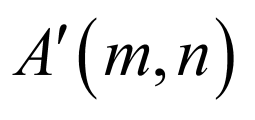 ,则有
,则有 ;
;
(2)直线关于直线的对称可转化为点关于直线的对称问题来解决.
运用向量的线性运用表示向量 ,对照系数,求得
,对照系数,求得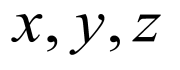 ,代入可得选项.
,代入可得选项.
【详解】
因为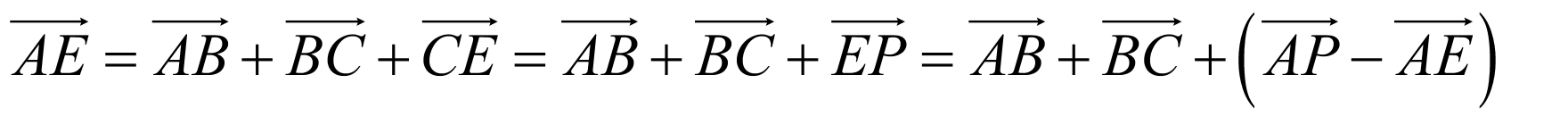 ,
,
所以 ,所以
,所以 ,所以
,所以 ,
,
解得 ,所以
,所以 ,
,
故选:B.
列举数列0,1,0,1,…判断选项A;列举 为常数列,判断选项B;列举
为常数列,判断选项B;列举 ,判断选项C;利用等差数列的定义判断选项D.
,判断选项C;利用等差数列的定义判断选项D.
【详解】
对于A,数列0,1,0,1,…的通项公式可以是 ,或
,或 ,命题错误;对于B,若
,命题错误;对于B,若 为常数列,则任何两项之和相等,结论不成立,命题错误﹔对于C,若
为常数列,则任何两项之和相等,结论不成立,命题错误﹔对于C,若 ,则
,则 ,数列
,数列 不是等比数列,命题错误;对于D,当
不是等比数列,命题错误;对于D,当 时,
时, ,结论成立,命题正确.
,结论成立,命题正确.
故选:D.
通过构造数列法得 ,
, 为等比数列,求得
为等比数列,求得 的通项公式,得到
的通项公式,得到 通项公式,结合分组求和法得出
通项公式,结合分组求和法得出 ,由单调性代值验证即可求解.
,由单调性代值验证即可求解.
【详解】
由原式 变形得
变形得 ,又
,又 ,所以
,所以 为等比数列,首项为4,公比为
为等比数列,首项为4,公比为 ,
, ,
, ,结合分组求和法得
,结合分组求和法得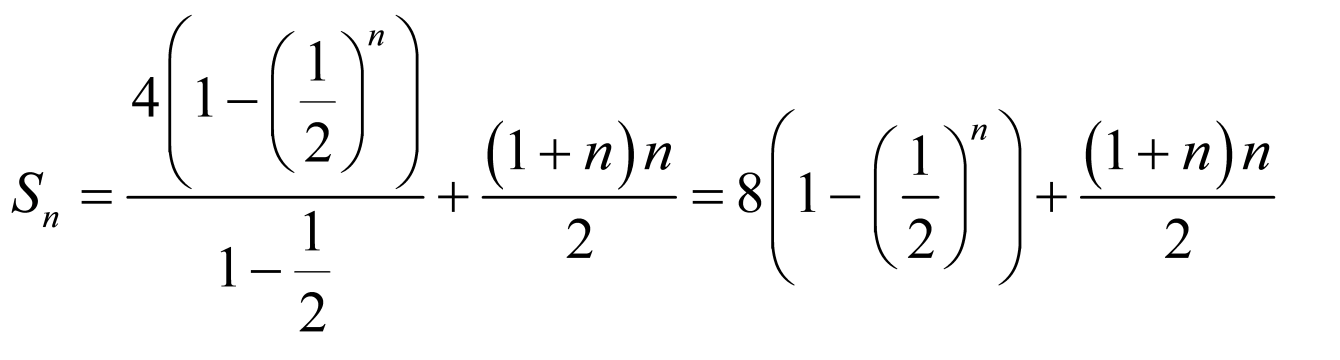 ,当
,当 时,
时, 为递增数列,
为递增数列, ,
, ,故
,故 的最小整数n的值是63.
的最小整数n的值是63.
故选:C
先求出三个平面的法向量,设两平面的交线的方向向量为 ,并求出其坐标,即得直线
,并求出其坐标,即得直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
【详解】
∵平面 的方程为
的方程为 ,
,
∴平面 的法向量可取
的法向量可取 ,
,
平面 的法向量为
的法向量为 ,
,
平面 的法向量为
的法向量为 ,
,
设两平面的交线的方向向量为 ,由
,由 ,则
,则 ,
,
则直线 与平面
与平面 所成角的平面角为
所成角的平面角为 ,
,
则 ,
,
故选:B.
设所求直线的方程为 ,解方程
,解方程 即得解.
即得解.
【详解】
设所求直线的方程为 ,即
,即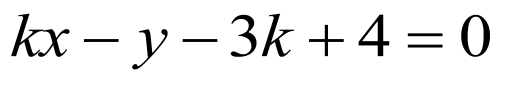 ,
,
由已知及点到直线的距离公式可得 ,
,
解得 或
或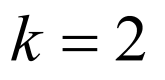 ,
,
即所求直线方程为 或
或 ,
,
故选:BC.
由题意可得圆心 到直线
到直线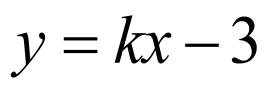 (
( )的距离大于2,利用点到直线的距离公式求得k的范围,可得结论.
)的距离大于2,利用点到直线的距离公式求得k的范围,可得结论.
【详解】
圆C的方程为 ,即
,即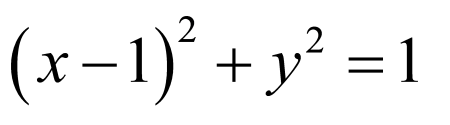 ,圆心
,圆心 ,半径为1,
,半径为1,
由题意可得,圆心 到直线
到直线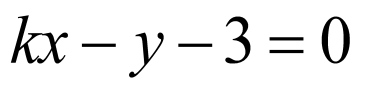 (
( )的距离大于2,
)的距离大于2,
即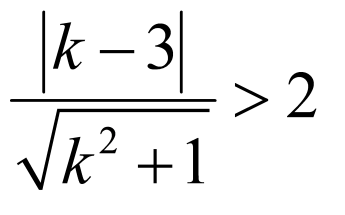 ,求得
,求得 ,∴
,∴ 或-1或0.
或-1或0.
故选:ABC.
【点睛】
本小题主要考查直线和圆的位置关系,考查圆与圆的位置关系,属于基础题.
由等比中项的性质和等差数列的通项公式可求得 ,再运用等差数列的求和公式求得
,再运用等差数列的求和公式求得 ,再逐一判断可得选项.
,再逐一判断可得选项.
【详解】
解:由 ,即
,即 ,
, ,得:
,得: ,
,
又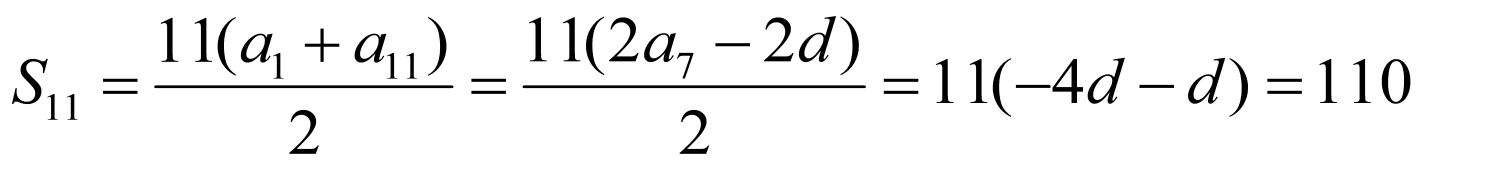 ,解得
,解得 ,所以B正确;
,所以B正确;
 ,所以A不正确;
,所以A不正确;
 ,
,
 ,当
,当 或11时,
或11时, 最大,所以C正确;
最大,所以C正确;
 时,即
时,即 ,解得
,解得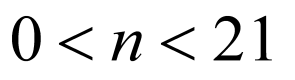 ,所以
,所以 时
时 的最大值为20,
的最大值为20,
所以D不正确,
故选:BC.
对于A,利用线线平行,将 与
与 的位置关系转换为判断
的位置关系转换为判断 与
与 的位置关系;
的位置关系;
对于B,作出辅助线:取 的中点
的中点 ,连接
,连接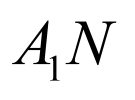 、
、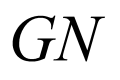 ,然后利用面面平行判断;
,然后利用面面平行判断;
对于C,把截面 补形为四边形
补形为四边形 ,由等腰梯形计算其面积判断;
,由等腰梯形计算其面积判断;
对于D,利用反证法判断.
【详解】
对于A,因为 ,若
,若 ,则
,则 ,从图中可以看出,
,从图中可以看出, 与
与 相交,但不垂直,所以A错误;
相交,但不垂直,所以A错误;
对于B,如图所示,取 的中点
的中点 ,连接
,连接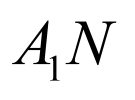 、
、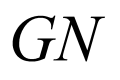 ,则有
,则有 ,
,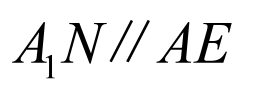 ,
,

∵ ,
,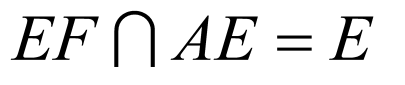 ,∴平面
,∴平面 ∥平面
∥平面 .
.
又∵ 平面
平面 ,∴
,∴ ∥平面
∥平面 ,故选项B正确;
,故选项B正确;
对于C,如图所示,连接 ,
, ,延长
,延长 ,
,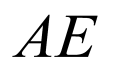 交于点
交于点 ,
,

∵ ,
,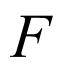 分别为
分别为 ,
, 的中点,∴
的中点,∴ ,
,
∴ 、
、 、
、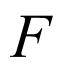 、
、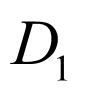 四点共面,∴截面即为梯形
四点共面,∴截面即为梯形 .
.
∵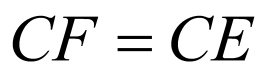 ,∴
,∴ ,即
,即 ,∴
,∴
又 ,∴
,∴ 即
即 ,
, ,
,
∴等腰△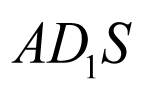 的高
的高 ,梯形
,梯形 的高为
的高为 ,
,
∴梯形 的面积为
的面积为 ,故选项C正确;
,故选项C正确;
对于D,假设 与
与 到平面
到平面 的距离相等,即平面
的距离相等,即平面 将
将 平分,则平面
平分,则平面 必过
必过 的中点,
的中点,
连接 交
交 于
于 ,而
,而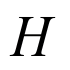 不是
不是 中点,则假设不成立,故D错.
中点,则假设不成立,故D错.
故选:BC﹒
先利用等比数列的性质通过 求出
求出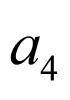 ,再根据条件可得
,再根据条件可得 ,进而根据等比数列的性质可得
,进而根据等比数列的性质可得 .
.
【详解】
 ,得
,得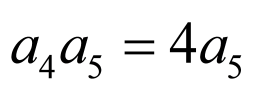
所以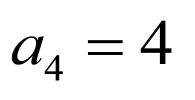 ,
,
 ,得
,得
因为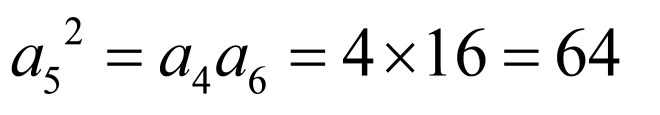 ,
,

故答案为: .
.
利用弦化切可求得结果.
【详解】
由已知可得 ,
,
因此,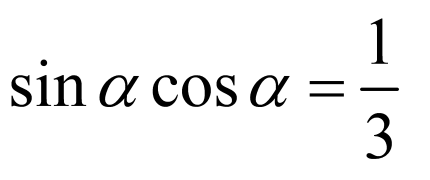 .
.
故答案为: .
.
由已知条件可得椭圆的标准方程是 ,再将直线与椭圆方程联立方程组,消去
,再将直线与椭圆方程联立方程组,消去 后,利用根与系数的关系结中点坐标公式可得答案
后,利用根与系数的关系结中点坐标公式可得答案
【详解】
由已知条件得椭圆的焦点在 轴上,其中
轴上,其中 ,
,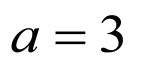 ,从而
,从而 ,
,
∴其标准方程是: ,
,
联立方程组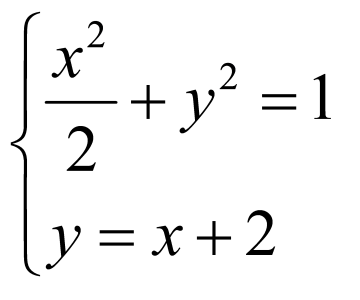 ,消去
,消去 得,
得, .
.
设 、
、 ,
, 线段的中点为
线段的中点为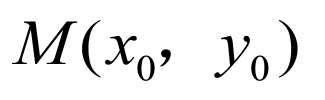 ,则
,则 ,
, ,
,
∴ ,即线段
,即线段 中点坐标为
中点坐标为 .
.
故答案为:
正方体 的棱上到直线
的棱上到直线 与
与 的距离相等的点分别为
的距离相等的点分别为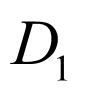 ,
, 的中点,
的中点, 的靠近
的靠近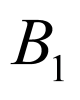 的四等分点,假设
的四等分点,假设 的中点为
的中点为 ,
, 的靠近
的靠近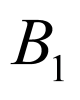 的四等分点为
的四等分点为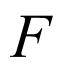 ,以
,以 为原点,
为原点, ,
, ,
, 所在直线分别为
所在直线分别为 ,
, ,
, 轴,建立空间直角坐标系,利用向量法能求出直线
轴,建立空间直角坐标系,利用向量法能求出直线 与平面
与平面 所成角的正切值.
所成角的正切值.
【详解】
解:正方体 的棱上到直线
的棱上到直线 与
与 的距离相等的点分别为:
的距离相等的点分别为:
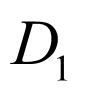 ,
, 的中点,
的中点, 的靠近
的靠近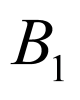 的四等分点,
的四等分点,
假设 的中点为
的中点为 ,
, 的靠近
的靠近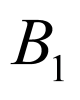 的四等分点为
的四等分点为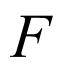 ,
,
以 为原点,
为原点, ,
, ,
, 所在直线分别为
所在直线分别为 ,
, ,
, 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
设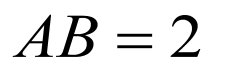 ,则
,则 ,2,
,2, ,
,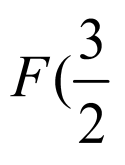 ,2,
,2, ,
, ,0,
,0, ,0,
,0, ,
,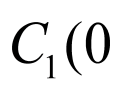 ,2,
,2, ,
,

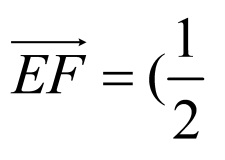 ,0,
,0, ,
, ,2,
,2,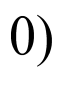 ,
, ,2,
,2, ,
,
设平面 的法向量
的法向量 ,
, ,
,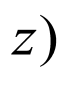 ,
,
则 ,令
,令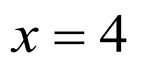 ,则
,则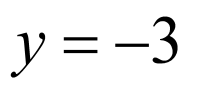 ,
, ,得
,得 ,
, ,
, ,
,
设直线 与平面
与平面 所成角为
所成角为 ,
,
则 ,
,
 ,
,
 直线
直线 与平面
与平面 所成角的正切值
所成角的正切值 .
.
故答案为: .
.

(1)利用勾股定理证得 ,结合线面垂直的判定定理即可证得结论;
,结合线面垂直的判定定理即可证得结论;
(2)以A为原点建立空间直角坐标系,设点 ,
, ,求得平面
,求得平面 的法向量
的法向量 ,利用已知条件建立关于
,利用已知条件建立关于 的方程,进而得解.
的方程,进而得解.
(1)
取 中点为
中点为 ,连接
,连接 ,
,
在 中,
中, ,
,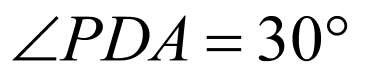 ,
, ,
,
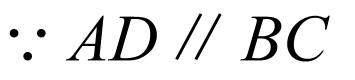 ,
, ,所以
,所以 ,
,
又 ,
, ,而
,而 ,所以
,所以 ,
,
又 ,
, ,
, ,
,
又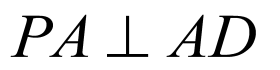 ,
,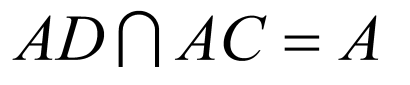 ,
, 平面
平面
(2)
存在点F是 的中点,使直线CF与平面PBC所成角的正弦值等于
的中点,使直线CF与平面PBC所成角的正弦值等于 .
.
以A为坐标原点,以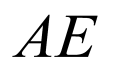 为x轴,
为x轴, 为y轴,
为y轴, 为z轴建立空间直角坐标系,
为z轴建立空间直角坐标系,
则 ,
, ,
, ,
, ,设点
,设点 ,
,
因为点F在线段 上,设
上,设 ,
,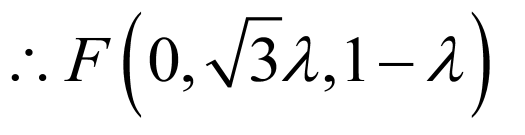 ,
,
 ,
,
设平面 的法向量为
的法向量为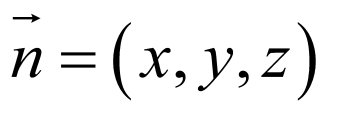 ,
,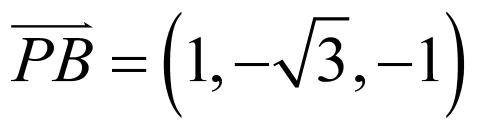 ,
,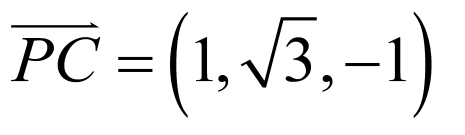
则 ,令
,令 ,则
,则
设直线CF与平面 所成角为
所成角为 ,
, ,
,
解得 或
或 (舍去),
(舍去),
,此时点F是 的中点,所以存在点F.
的中点,所以存在点F.
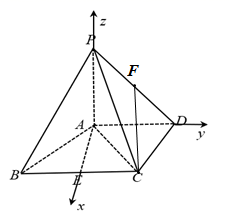
(1)由题可设 ,则
,则 ,即求;
,即求;
(2)利用等比数列求和公式及裂项相消法可得 ,然后由
,然后由 判断数列的单调性,即得.
判断数列的单调性,即得.
(1)
由题可设 ,由
,由 ,
, ,
, 成等差数列,
成等差数列,
则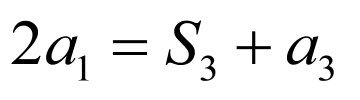 ,即
,即 ,
,
∴ ,
,
解得 ,
,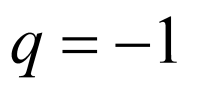 (舍去),
(舍去),
故数列 的通项公式为
的通项公式为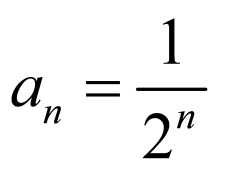 .
.
(2)
∵ ,
,
∴ ,又
,又 ,
,
设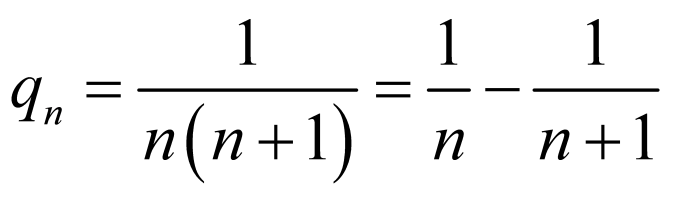 ,且数列
,且数列 的前
的前 项和为
项和为 ,
,
则 ,
,
所以 .
.
令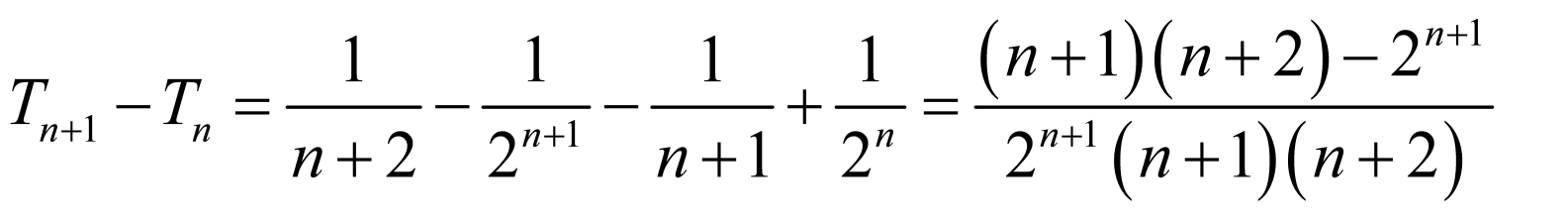 ,
,
随着 的变化,比较
的变化,比较 与
与 变化速度,令
变化速度,令 ,可得
,可得 ,
,
即 ,
, ,
, ,
,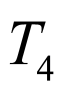 递增,而
递增,而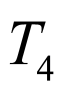 ,
, ,
, ,
, ,
, 递减,
递减,
所以 最大,最大值
最大,最大值 .
.
故 的最大值为
的最大值为 .
.
(1)通过构造中位线的方法来证得 平面
平面 .
.
(2)建立空间直角坐标系,利用向量法来求二面角 的余弦值.
的余弦值.
(3)设 ,根据
,根据 列方程,化简求得
列方程,化简求得 的值.
的值.
(1)
连接 交
交 于
于 ,连接
,连接 ,
,
由于 分别是
分别是 的中点,所以
的中点,所以 ,
,
由于 平面
平面 ,
, 平面
平面 ,
,
所以 平面
平面 .
.
(2)
以 为空间坐标原点建立如图所示空间直角坐标系,设
为空间坐标原点建立如图所示空间直角坐标系,设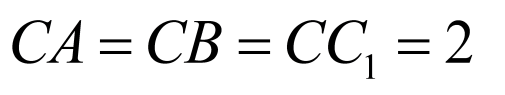 ,
,
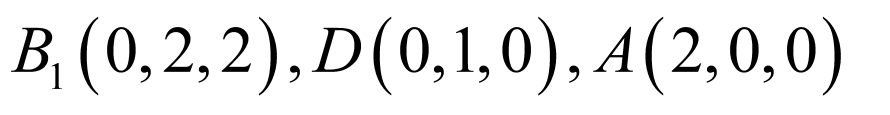 ,
, ,
,
设平面 的法向量为
的法向量为 ,
,
则 ,故可设
,故可设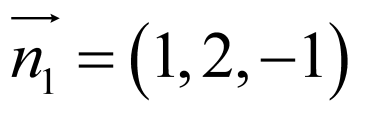 ,
,
平面 的法向量为
的法向量为 ,
,
设二面角 的平面角为
的平面角为 ,由图可知,
,由图可知, 为锐角,
为锐角,
所以 .
.
(3)
 ,
,
设 ,
, ,即
,即 ,
,
 ,
,
 ,
,
由于 ,所以
,所以 .
.

(1)令 ,临界条件为直线
,临界条件为直线 与圆相切,利用圆心到直线的距离等于半径,求得
z的取值范围,进而得解;
与圆相切,利用圆心到直线的距离等于半径,求得
z的取值范围,进而得解;
(2)利用圆的弦长公式及 ,可求实数m的值.
,可求实数m的值.
(1)
将圆的方程变形为 ,圆心
,圆心
 ,
,
令 ,即
,即 ,
,
如图,临界条件为直线与圆相切,当直线为 位置时取
位置时取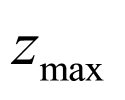 ,当直线为
,当直线为 位置时取
位置时取

圆心到直线的距离 ,即
,即
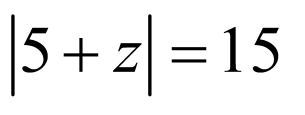 ,解得
,解得 或
或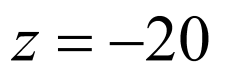
所以 的取值范围为
的取值范围为
(2)
 ,
,

圆心到直线的距离
由点到直线的距离公式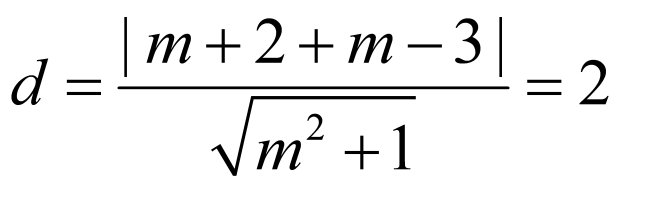 ,即
,即
 ,解得
,解得
所以实数m的值为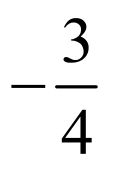
(1)讨论 、
、 求
求 成立时
成立时 的取值范围;
的取值范围;
(2)根据不等式的解集可得 ,则原问题为
,则原问题为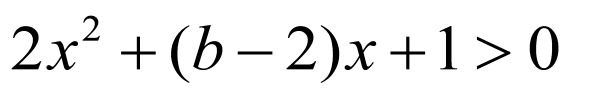 在
在 上恒成立,由
上恒成立,由 求
求 的取值范围.
的取值范围.
(1)
当 时,可得
时,可得 ,即
,即 成立;
成立;
当 时,若
时,若 成立,则
成立,则 ,可得
,可得 且
且 .
.
综上, .
.
(2)
由题设, 在
在 上恒成立,
上恒成立,
由 ,知:
,知: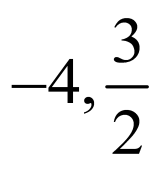 是
是 的两个根且
的两个根且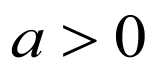 ,
,
∴ ,可得
,可得 ,
,
综上,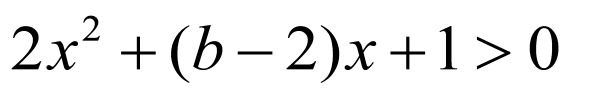 在
在 上恒成立,则
上恒成立,则 ,
,
∴ .
.
(1)由点到直线距离公式,离心率公式列出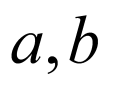 的方程组解之可筣可退回方程;
的方程组解之可筣可退回方程;
(2)设直线 的方程为
的方程为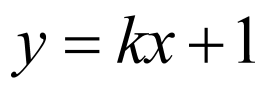 ,代入椭圆方程由判别式为0得
,代入椭圆方程由判别式为0得 关系,从而得
关系,从而得 ,再回代求得
,再回代求得 点坐标,写出
点坐标,写出 方程,求得
方程,求得 点坐标,计算
点坐标,计算 可得结论.
可得结论.
(1)
由题意,得点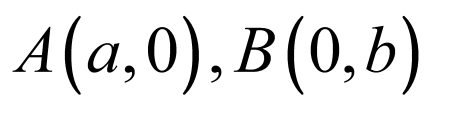 ,直线
,直线 的方程为
的方程为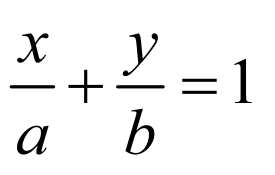 ,即
,即 ,
,
由题设,得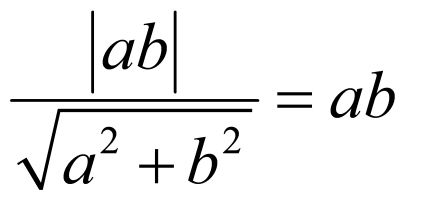 ,化简,得
,化简,得 ①
①
 ,即
,即 ,②
,②
由①②解得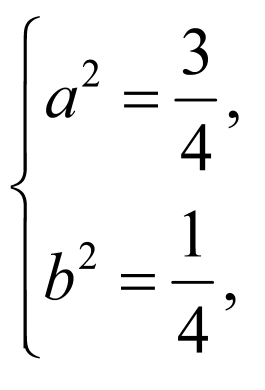
所以,椭圆 的方程为
的方程为 .
.
(2)
点 在以
在以 为直径的圆上.理由如下:
为直径的圆上.理由如下:
由题设,直线 与椭圆相切且
与椭圆相切且 的斜率存在,设直线
的斜率存在,设直线 的方程为:
的方程为: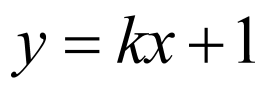 ,
,
由 得
得
则 ,化简得
,化简得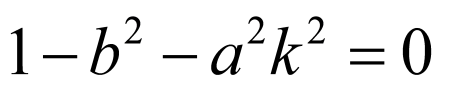 ,
,
由(1)得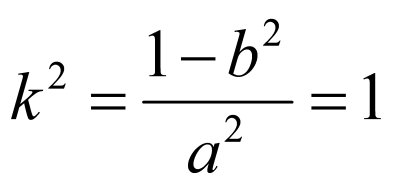 ,
,
 点
点 在第二象限,
在第二象限, .
.
把 代入方程
代入方程 ,得
,得 ,
,
解得 ,从而
,从而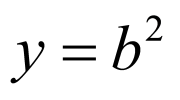 ,所以
,所以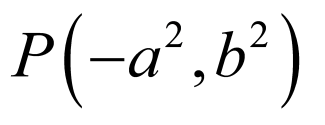 .
.
从而直线 的方程为:
的方程为: ,
,
令 ,得
,得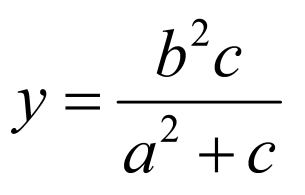 ,所以点
,所以点 ,
,
从而 ,
,
从而 ,
,
又 ,
,
所以点 在以
在以 为直径的圆上.
为直径的圆上.
第九张
求出当命题“ ,
, ”是真命题时,实数
”是真命题时,实数 的取值范围,结合题意可得出合适的选项.
的取值范围,结合题意可得出合适的选项.
【详解】
命题“ ,
, ”是真命题,则
”是真命题,则 ,
,
因此,命题“ ,
, ”是真命题的一个必要不充分条件是
”是真命题的一个必要不充分条件是 .
.
故选:A.
求出 的范围,根据
的范围,根据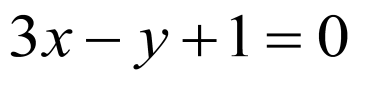 ,
, 的意义求解即可.
的意义求解即可.
【详解】
由 ,解得
,解得 .
.
因为 ,所以
,所以 或
或 .
.
故 表示一条线段.
表示一条线段.
因为 ,所以
,所以 ,
, ,即
,即 表示以原点为圆心的半个圆
表示以原点为圆心的半个圆
故选:C
利用等差数列通项公式和前 项和公式列方程组,求出首项和公差,由此能求出结果.
项和公式列方程组,求出首项和公差,由此能求出结果.
【详解】
解:设数列为 ,首项为
,首项为 ,公差为
,公差为 ,
,
则 ,
,
 ,
,
解得 ,
, ,
,
 芒种日影长为
芒种日影长为 .
.
故选:B.
设出正四面体的棱长,根据向量的加减法表示出 ,然后利用
,然后利用 即可求解;
即可求解;
【详解】
设正四面体的棱长为 ,则
,则 ,
,


 为正四面体,
为正四面体, 均为正三角形,
均为正三角形,
 ,
,
 ,
,
 ,异面直线
,异面直线 与
与 所成角的余弦值为
所成角的余弦值为 .
.
故选:B
由 可得
可得 ,两式相减得
,两式相减得 ,则
,则 ,从而可求得
,从而可求得 ,再利用裂项相消法即可求出答案.
,再利用裂项相消法即可求出答案.
【详解】
解:由 ,得
,得 ,
,
两式相减得 ,则
,则 ,
,
又当 时,
时, ,解得
,解得 ,满足上式,
,满足上式,
所以 ,
,
所以 ,
,
所以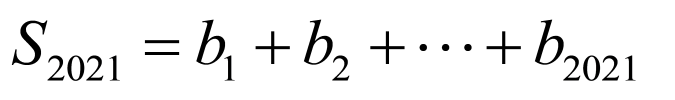

 .
.
故选:C.
据题意分析可知直线经过定点 ;圆的圆心到直线距离的最大时,圆的半径最大,即可得到面积最大的圆的标准方程.
;圆的圆心到直线距离的最大时,圆的半径最大,即可得到面积最大的圆的标准方程.
【详解】
 直线方程为:
直线方程为: 可化为
可化为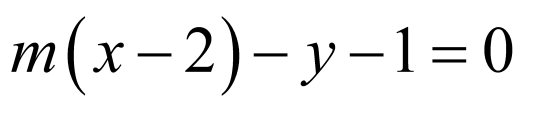 ,
,
 直线经过定点
直线经过定点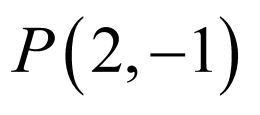 ,
,
易知: 圆的半径最大时,圆的面积最大,
圆的半径最大时,圆的面积最大, 圆心到直线的距离最大时圆的面积最大,
圆心到直线的距离最大时圆的面积最大,
又 动圆
动圆 ,圆心为
,圆心为 ,半径为
,半径为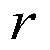 ,
,
 当
当 与已知直线垂直时圆的半径最大,
与已知直线垂直时圆的半径最大, ,
,
 面积最大的圆的标准方程为:
面积最大的圆的标准方程为: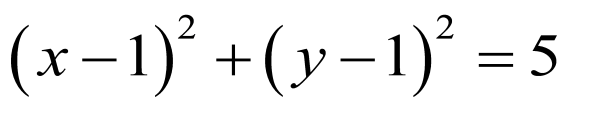 .
.
故选:B
根据双曲线与抛物线共焦点,可确定双曲线的半焦距,再根据双曲线的性质及三角形 的面积可得
的面积可得 或
或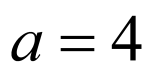 ,进而可得离心率.
,进而可得离心率.
【详解】

 抛物线
抛物线 的交点坐标为
的交点坐标为 ,
,
又双曲线 与抛物线
与抛物线 共焦点,
共焦点,
 双曲线的半焦距
双曲线的半焦距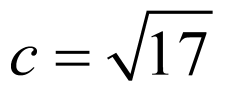 ,
,
 三角形
三角形 的面积为
的面积为 ,且
,且 ,
,

 ,即
,即 ,
,
有 ,
,

 或
或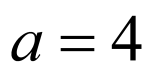 ,
,
 双曲线的离心率为
双曲线的离心率为 或
或 ,
,
故选:C.
记椭圆的左焦点为 ,根据
,根据 和
和 ,结合椭圆的定义求出a的范围,进而求出离心率的范围.
,结合椭圆的定义求出a的范围,进而求出离心率的范围.
【详解】
记椭圆的左焦点为 ,连接
,连接 ,则
,则 即
即
 所以椭圆
所以椭圆 的圆心率的取值范围是
的圆心率的取值范围是 .
.
故选:A.
首先求出 ,
, ,
, ,即可得到
,即可得到 ,从而判断A、B,再根据平面向量数量积的坐标表示得到
,从而判断A、B,再根据平面向量数量积的坐标表示得到 且
且 ,即可判断C,最后求出平面
,即可判断C,最后求出平面 的法向量,利用空间向量法求出线面角的正弦值;
的法向量,利用空间向量法求出线面角的正弦值;
【详解】
解:因为 ,
, ,
, ,
, ,
, ,
,
所以 ,
,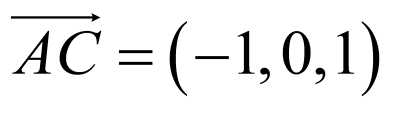 ,
, ,所以
,所以 ,故A错误;
,故A错误;
设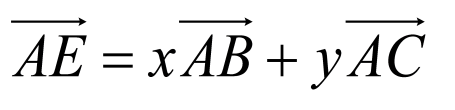 ,即
,即 ,解得
,解得 ,即
,即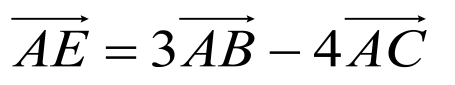 ,
,
设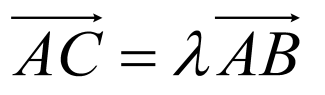 ,即
,即 ,即
,即 ,显然
,显然 无解,即
无解,即 与
与 不共线,所以
不共线,所以 ,
, ,
, ,
, 四点共面,故B正确;
四点共面,故B正确;
因为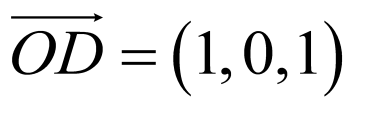 ,所以
,所以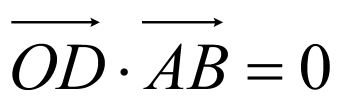 ,
, ,所以
,所以 且
且 ,所以向量
,所以向量 是平面
是平面 的一个法向量,故C正确;
的一个法向量,故C正确;
设平面 的法向量为
的法向量为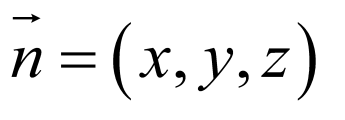 ,所以
,所以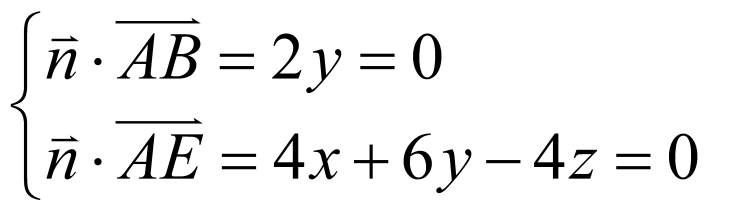 ,令
,令 ,则
,则 ,
, ,所以
,所以 ,又
,又 ,设
,设 与平面
与平面 所成角为
所成角为 ,所以
,所以 ,即
,即 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,故D错误;
,故D错误;
故选:BC
对选项进行逐一判断.由椭圆的定义判断A;由 为定值以及
为定值以及 的范围判断B;求出
的范围判断B;求出 坐标,由数量积公式得出
坐标,由数量积公式得出 ,得出
,得出 为直角三角形判断C;求出
为直角三角形判断C;求出 坐标,由面积公式得出
坐标,由面积公式得出 的面积判断D.
的面积判断D.
【详解】
设椭圆的左焦点为 ,则
,则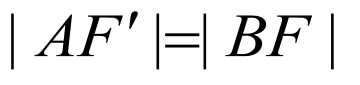
所以 为定值,A正确;
为定值,A正确;
 的周长为
的周长为 ,因为
,因为 为定值6,
为定值6,
所以 的范围是
的范围是 ,所以
,所以 的周长的范围是
的周长的范围是 ,B错误;
,B错误;
将 与椭圆方程联立,可解得
与椭圆方程联立,可解得 ,
,
又因为 ,∴
,∴
所以 为直角三角形,C正确;
为直角三角形,C正确;
将 与椭圆方程联立,解得
与椭圆方程联立,解得 ,
, ,所以
,所以 ,D正确.
,D正确.
故选:ACD
根据给定条件求出函数 的解析式,进而求出
的解析式,进而求出 的含有数0的单调区间,再借助集合的包含关系列式作答.
的含有数0的单调区间,再借助集合的包含关系列式作答.
【详解】
依题意,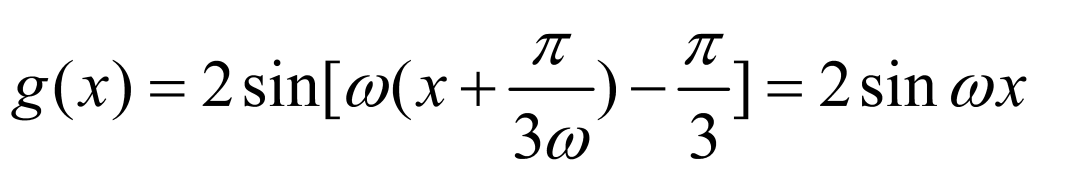 ,由
,由 ,
,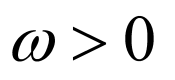 得:
得: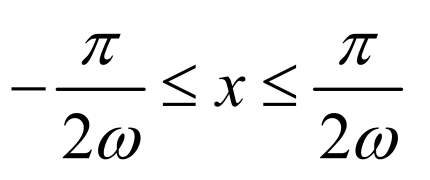 ,
,
于是得 的一个单调递增区间是
的一个单调递增区间是 ,因
,因 在
在 上为增函数,
上为增函数,
因此, ,即有
,即有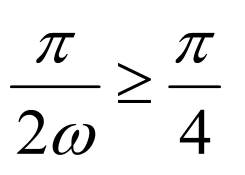 ,解得
,解得 ,
,
所以,选项C,D不满足,选项A,B满足.
故选:AB
结合双曲线的定义和条件可得 ,然后
,然后 ,然后逐一判断即可.
,然后逐一判断即可.
【详解】
由双曲线的定义可得 ,
,
因为 ,所以
,所以 ,故A错误;
,故A错误;
因为以线段 为直径的圆与双曲线在第一象限的交点为
为直径的圆与双曲线在第一象限的交点为 ,
,
所以 ,所以
,所以 的面积为
的面积为 ,故B正确;
,故B正确;
由勾股定理得 ,即
,即 ,所以
,所以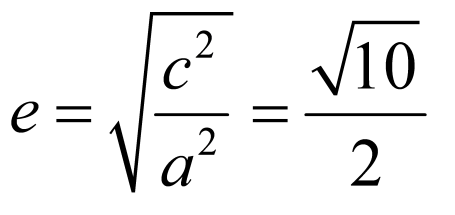 ,故C正确
,故C正确
因为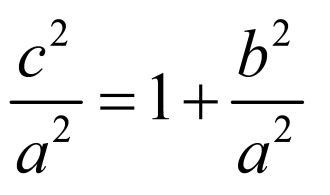 ,所以
,所以 ,即
,即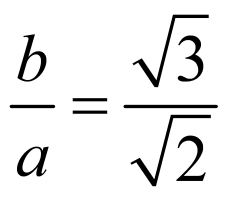
所以双曲线的渐近线方程为: ,即
,即 ,即
,即 ,故D正确
,故D正确
故选:BCD
利用空间向量的线性运算即得.
【详解】
∵D为BC的中点, ,点E为AD中点,
,点E为AD中点,

∴ .
.
故答案为: .
.
计算故以 为圆心,
为圆心,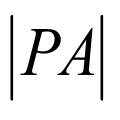 为半径的圆方程,两圆方程相减得到答案.
为半径的圆方程,两圆方程相减得到答案.
【详解】
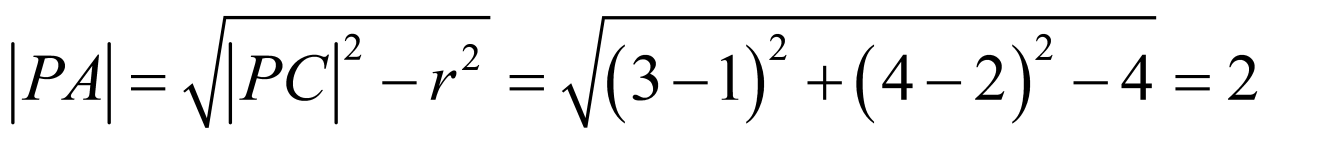 ,
,
故以 为圆心,
为圆心,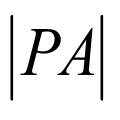 为半径的圆为
为半径的圆为 ,
,
两圆方程相减得到 即为直线
即为直线 方程.
方程.
故答案为: .
.
设点 为第一象限内的点,设椭圆与双曲线的焦点都在
为第一象限内的点,设椭圆与双曲线的焦点都在 轴上,设椭圆的长轴长为
轴上,设椭圆的长轴长为 ,双曲线的实轴长为
,双曲线的实轴长为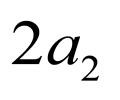 ,两曲线的焦距为
,两曲线的焦距为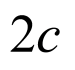 ,椭圆和双曲线的离心率分别为
,椭圆和双曲线的离心率分别为 、
、 ,利用余弦定理、椭圆和双曲线的定义可得出
,利用余弦定理、椭圆和双曲线的定义可得出 ,进而可得出
,进而可得出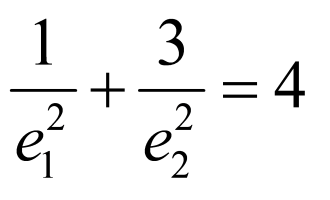 ,结合
,结合 可求得
可求得 的值,即可得解.
的值,即可得解.
【详解】
设椭圆与双曲线的焦点都在 轴上,设椭圆的长轴长为
轴上,设椭圆的长轴长为 ,双曲线的实轴长为
,双曲线的实轴长为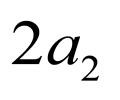 ,两曲线的焦距为
,两曲线的焦距为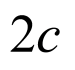 ,椭圆和双曲线的离心率分别为
,椭圆和双曲线的离心率分别为 、
、 ,
,
不妨设 为第一象限的点,
为第一象限的点,

在椭圆中: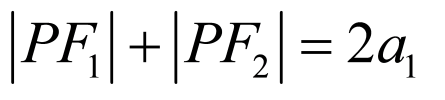 ①,在双曲线中:
①,在双曲线中: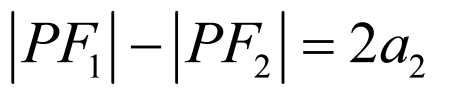 ②,
②,
联立①②解得, ,
, ,
,
在 中由余弦定理得:
中由余弦定理得: ,
,
即
即 ,即
,即 ,所以,
,所以,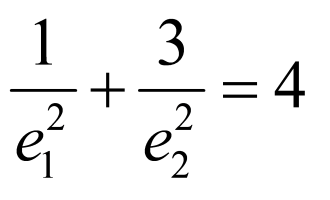 ,
,
因为椭圆的离心率 ,所以双曲线的离心率
,所以双曲线的离心率 ,
,
故答案为: .
.
【点睛】
方法点睛:求解椭圆或双曲线的离心率的方法如下:
(1)定义法:通过已知条件列出方程组,求得 、
、 的值,根据离心率的定义求解离心率
的值,根据离心率的定义求解离心率 的值;
的值;
(2)齐次式法:由已知条件得出关于 、
、 的齐次方程,然后转化为关于
的齐次方程,然后转化为关于 的方程求解;
的方程求解;
(3)特殊值法:通过取特殊位置或特殊值,求得离心率.
做出曲线 的图象,结合直线
的图象,结合直线 过定点
过定点 ,数形结合即可求出结果.
,数形结合即可求出结果.
【详解】
由题意可知,曲线 表示圆心为
表示圆心为 ,半径为1的圆的上半部分(含端点),则直线
,半径为1的圆的上半部分(含端点),则直线 与曲线
与曲线 有两个不同的公共点时,且直线
有两个不同的公共点时,且直线 过定点
过定点 ,
,

可考虑临界状态,即直线与半圆相切时或直线经过点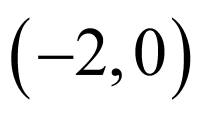 ,
,
当过点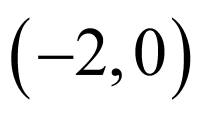 时,
时, ,即
,即 ,
,
当直线 与圆相切时,
与圆相切时, ,解得
,解得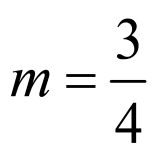 ,
,
数形结合可知有两个不同的公共点时实数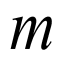 的取值范围为
的取值范围为 .
.
故答案为: .
.
(1)设出圆的半径,根据圆的弦长公式可求出半径,即可写出圆C的标准方程;
(2)当斜率不存在时,检验是符合;当斜率存在时,由点斜式设出直线方程,根据直线与圆相切,即可求出斜率,得到直线方程.
【详解】
(1)根据题意,设圆C的方程为 ,
,
因为圆C被直线 截得的弦长为
截得的弦长为 ,圆心
,圆心 到直线
到直线 的距离为
的距离为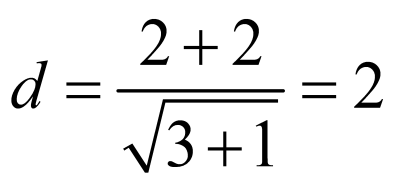 ,则
,则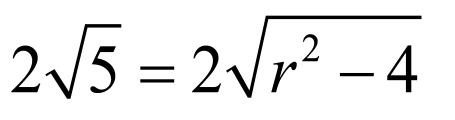 ,解得
,解得 .
.
则圆C的标准方程为 .
.
(2)当斜率不存在时,直线 的方程为
的方程为 ,
,
显然圆心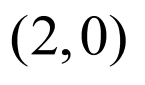 到
到 的距离为3,正好等于半径,符合题意;
的距离为3,正好等于半径,符合题意;
当斜率存在时,设斜率为k,则过M点的直线方程为: ,
,
即 ,圆心到直线的距离等于半径3,
,圆心到直线的距离等于半径3,
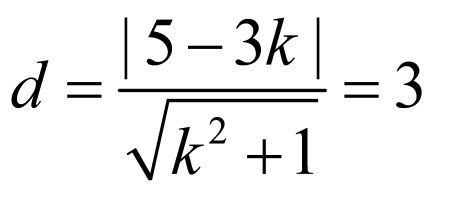 ,解得
,解得 ,
,
所以直线 的方程为
的方程为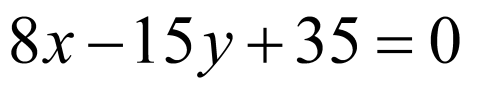 .
.
综上,所求的直线方程为 或
或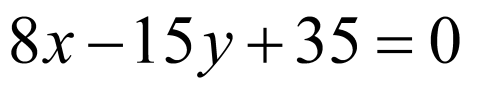 .
.
【点睛】
本题主要考查圆的方程求法以及直线与圆的位置关系的应用,注意分类讨论思想的应用,属于基础题.
(1)证明见解析;
(2) ,
, .
.
【分析】
(1)由题设可得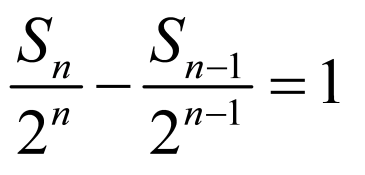 ,即可证明结论;
,即可证明结论;
(2)由(1)可知 ,再根据
,再根据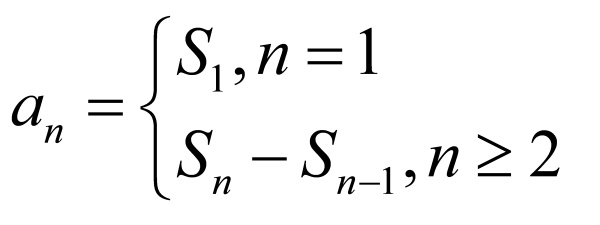 计算可得;
计算可得;
(1)
由 ,
, ,
,
∴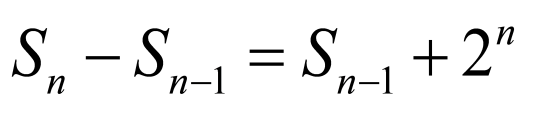 ,整理得:
,整理得: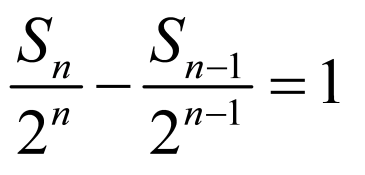 ,而
,而 ,
,
∴ 以
以 为首项,1为公差的等差数列,得证.
为首项,1为公差的等差数列,得证.
(2)
由(1)得: ,
,
①当 时,
时, ;
;
②当 时,
时, ,
,
综上, 时
时 成立,
成立,
∴ ,
, .
.
(1)连接BE,BF,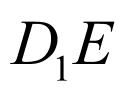 ,
, ,取
,取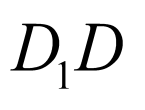 中点
中点 ,连接
,连接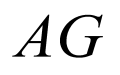 、
、 ,证明四边形
,证明四边形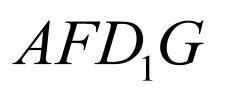 为平行四边形,证明
为平行四边形,证明 ,可得
,可得 ,同理可得,
,同理可得, ,进而有四边形
,进而有四边形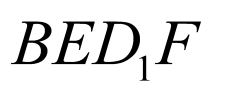 为平行四边形,得证;
为平行四边形,得证;
(2)取AB的中点M,连接DM,易证 ,再以D为原点建立空间直角坐标系,求得平面
,再以D为原点建立空间直角坐标系,求得平面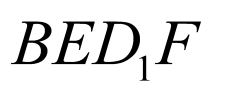 的法向量
的法向量 ,设直线AE与平面
,设直线AE与平面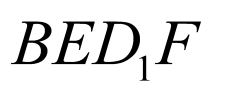 所成角为
所成角为 ,由
,由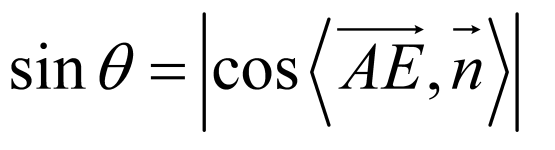 ,得解.
,得解.
(3)根据(2)中平面 的法向量
的法向量 ,利用点到平面的距离公式,即可求得
,利用点到平面的距离公式,即可求得 到平面
到平面 的距离.
的距离.
【详解】
解:(1)证明:连接BE,BF, ,
, ,
,
取 中点
中点 ,连接
,连接 、
、 ,
,
因为 分别为
分别为 、
、 中点,易得
中点,易得 ,
,
 ,
, ,且
,且 ,
,
 四边形
四边形 为平行四边形,
为平行四边形,
 ,又
,又 是
是 中点,
中点,
 ,
, ,则四边形
,则四边形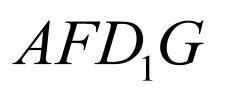 为平行四边形,
为平行四边形,
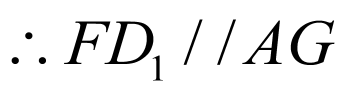 ,
,

因为 ,
, ,
, ,
,
所以 ,所以
,所以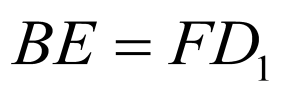 ,
,
所以四边形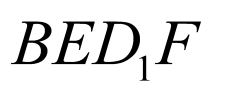 为平行四边形,
为平行四边形,
所以B,E,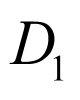 ,F四点共面.
,F四点共面.
(2)取AB的中点M,连接DM,
且 ,
, 为等边三角形,
为等边三角形,
所以 ,
, ,
,
以D为原点,DM, ,
, 所在直线分别为x,y,z轴,
所在直线分别为x,y,z轴,
由 ,则
,则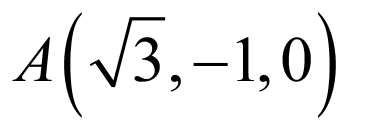 ,
,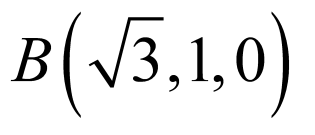 ,
, ,
,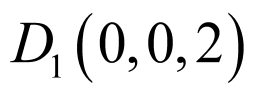 ,
,
所以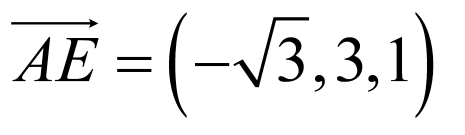 ,
, ,
,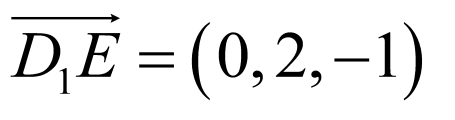 ,
,

设平面 的法向量为
的法向量为 ,
,
则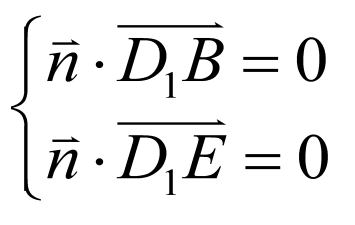 ,即
,即 ,
,
令 ,则
,则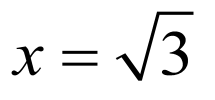 ,
, ,
,
设直线AE与平面 所成角为
所成角为 ,
,
则 ,
,
故直线AE与平面 所成角的正弦值为
所成角的正弦值为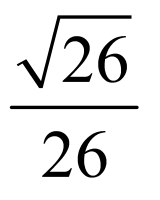 ;
;
(3)由 ,则
,则 ,
,
 到平面
到平面 的距离
的距离 ,
,
所以 到平面
到平面 的距离
的距离 .
.
(1)由对数的性质列不等式组求x的范围,即可得y= 定义域;
定义域;
(2)根据函数奇偶性的定义判断 的奇偶性;
的奇偶性;
(3)化简函数 的解析式为
的解析式为 ,结合已知及函数的奇偶性及区间单调性可得
,结合已知及函数的奇偶性及区间单调性可得 ,由此求得m的范围.
,由此求得m的范围.
(1)
由对数的性质知: ,即
,即 ,
,
∴ 的定义域为
的定义域为 .
.
(2)
由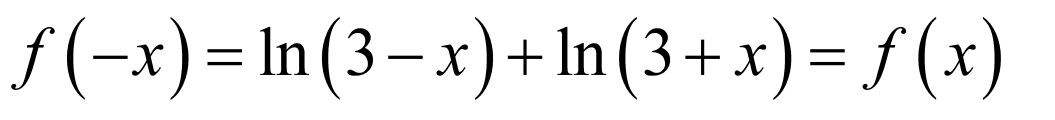 ,结合(1)所得的定义域,
,结合(1)所得的定义域,
∴ 偶函数.
偶函数.
(3)
∵ ,
,
∴ 是[0,3
是[0,3 上的减函数,又
上的减函数,又 是偶函数.
是偶函数.
∴ ,解得:
,解得: 或
或 .
.
(1)根据已知条件可得出关于 、
、 、
、 的方程组,解出这三个量的值,即可得出椭圆
的方程组,解出这三个量的值,即可得出椭圆 的方程;
的方程;
(2)由直线与圆相切可得出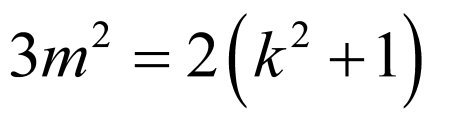 ,将直线
,将直线 的方程与椭圆方程联立,列出韦达定理,利用平面向量数量积的坐标运算结合韦达定理计算得出
的方程与椭圆方程联立,列出韦达定理,利用平面向量数量积的坐标运算结合韦达定理计算得出 ,即可求得结果.
,即可求得结果.
(1)
解:由已知可得 ,解得
,解得 ,故椭圆
,故椭圆 的方程为
的方程为 .
.
(2)
解:因为直线 与圆
与圆 相切,且直线
相切,且直线 的方程为
的方程为 ,
,
所以 ,即
,即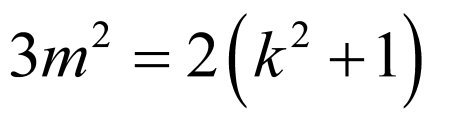 ,
,
联立 ,整理得
,整理得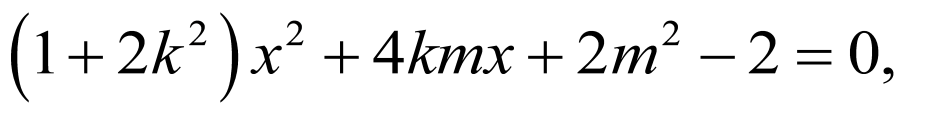 ,
,
 ,
,
设 、
、 ,则
,则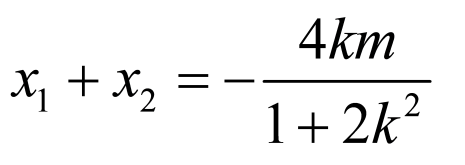 ,
, .
.
故 ,
,
则 ,故
,故 .
.
(1)根据焦距、双曲线上的点求双曲线参数,进而写出双曲线C的方程;
(2)由题设有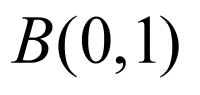 ,设直线
,设直线 为
为 ,
, ,并联立双曲线方程,应用韦达定理、中点坐标公式求M,N的中点坐标,由等腰三角形中垂线性质求参数k,进而可得直线l的方程.
,并联立双曲线方程,应用韦达定理、中点坐标公式求M,N的中点坐标,由等腰三角形中垂线性质求参数k,进而可得直线l的方程.
(1)
由题设, ,又
,又 在双曲线上,
在双曲线上,
∴ ,可得
,可得 ,
,
∴双曲线C的方程为 .
.
(2)
由(1)知: ,
,
直线 的斜率一定存在,当直线斜率为0时,直线
的斜率一定存在,当直线斜率为0时,直线 :
: ,符合题意;
,符合题意;
设直线 为
为 ,
, ,
,
联立双曲线方程可得: ,
,
由题设 ,
,
∴ ,
, ,则
,则 .
.
要使△ 构成以
构成以 为顶角的等腰三角形,则
为顶角的等腰三角形,则 ,
,
∴ 的中点坐标为
的中点坐标为 ,
,
∴ ,可得
,可得 或
或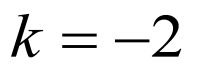 ,
,
当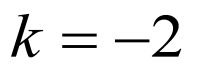 时,
时, ,不合题意,所以
,不合题意,所以 ,直线l:
,直线l: ,
,
∴存在直线 为
为 或
或 ,使△
,使△ 构成以
构成以 为顶角的等腰三角形
为顶角的等腰三角形
物理
第一张
多选题
1.
若物体的动能发生了变化,则速度的大小一定变化,但是物体的加速度不一定发生变化,例如物体做平抛运动,选项A错误;若物体的动能不变,则速度的大小不变,但是动量不一定不变,例如物体做匀速圆周运动,选项B错误;若一个系统所受的合外力为零,则该系统的动能不一定不变,例如子弹射入放在光滑水平面的木块中时,选项C错误;根据动量定理可知,F= ,即物体所受合外力越大,它的动量变化就越快,选项D正确.
,即物体所受合外力越大,它的动量变化就越快,选项D正确.
先伸出两臂迎接,手接触到球后,两臂随球引至胸前,这样可以增加球与手接触的时间,根据动量定理得:-Ft=0-mv,F= ,当时间增加时,动量的变化量不变,则手对球的作用力减小,由牛顿第三定律可知,球对手的作用力减小,所以B正确.
,当时间增加时,动量的变化量不变,则手对球的作用力减小,由牛顿第三定律可知,球对手的作用力减小,所以B正确.
4.
小球与地面碰撞过程中动量的变化量Δp=mv2-mv1=0.2×4 kg·m/s-0.2×(-6) kg·m/s=2 kg·m/s,方向竖直向上;由动能定理知,合外力做的功W= mv
mv -
- mv
mv =
= ×0.2×42 J-
×0.2×42 J- ×0.2×62 J=-2 J,故选A.
×0.2×62 J=-2 J,故选A.
6.
由题图图像可知,在前10 s内初、末状态的动量相同,p1=p2=5 kg·m/s,由动量定理知I1=0;在后10 s内末状态的动量p3=-5 kg·m/s,由动量定理得I2=p3-p2=-10 N·s,故选项D正确.
7. 根据自由落体运动公式得v= =
=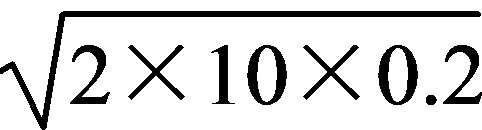 m/s=2 m/s,选取向上为正方向,手机与眼睛作用后手机的速度变为0,所以手机与眼睛作用过程中动量变化量为Δp=0-(-mv)=0.12×2 kg·m/s=0.24 kg·m/s,故A错误;手机与眼睛接触的过程中受到重力与眼睛的作用力,则:Iy-mgt=Δp,代入数据可得:Iy=0.48 N·s,手机对眼睛的作用力与眼睛对手机的作用力大小相等,方向相反,作用的时间相等,所以手机对眼睛的冲量大小约为0.48 N·s,方向竖直向下,故B正确,C错误;由冲量的定义得:Iy=Ft,可得:F=
m/s=2 m/s,选取向上为正方向,手机与眼睛作用后手机的速度变为0,所以手机与眼睛作用过程中动量变化量为Δp=0-(-mv)=0.12×2 kg·m/s=0.24 kg·m/s,故A错误;手机与眼睛接触的过程中受到重力与眼睛的作用力,则:Iy-mgt=Δp,代入数据可得:Iy=0.48 N·s,手机对眼睛的作用力与眼睛对手机的作用力大小相等,方向相反,作用的时间相等,所以手机对眼睛的冲量大小约为0.48 N·s,方向竖直向下,故B正确,C错误;由冲量的定义得:Iy=Ft,可得:F= =
= N=2.4 N,故D错误.
N=2.4 N,故D错误.
根据动量定理得:
0~t0内:F0t0=mv1
t0~2t0内:2F0t0=mv2-mv1
解得:v1∶v2=1∶3
由p=mv得:p2=3p1
由Ek= mv2得:Ek1=
mv2得:Ek1= mv
mv ,Ek2=
,Ek2= mv
mv
解得:Ek2=9Ek1,故选C.
9.这是“等时圆”模型,即三个滑环同时由静止释放,运动到最低点d点的时间相同,由于三个环的重力相等,由公式I=Ft分析可知,三个环重力的冲量相同,故A正确;从c处下滑的小滑环受到的弹力最大,运动时间相等,则弹力对从c处下滑的小滑环的冲量最大,故B错误;从a处下滑的小滑环的加速度最大,受到的合力最大,则合力对从a处下滑的小滑环的冲量最大,故C错误;重力对从a处下滑的小滑环做功最多,其动能的增量最大,故D错误.
10. 设子弹穿过每个水球的距离为d,子弹在水球中做匀减速直线运动,穿出第4个水球时,其末速度为零,我们可以把子弹的运动视为反向的初速度为零的匀加速直线运动,则子弹穿过最后1个、最后2个、最后3个、全部的4个水球的位移大小分别为d、2d、3d、4d,根据x= at2知,这4段位移对应的时间之比为1∶
at2知,这4段位移对应的时间之比为1∶ ∶
∶ ∶2,所以子弹在每个水球中运动的时间不同,子弹在水球中沿水平方向做匀变速直线运动,则子弹在每个水球中加速度相同,受力相同,由Δv=at及子弹在每个水球中运动的时间不同可知,子弹在每个水球中速度的变化量不同,选项A、C错误;子弹在每个水球中受力是相同的,运动的位移相同,所以子弹受到的阻力对子弹做的功相等,根据动能定理ΔEk=W=Fd,可知子弹在每个水球中的动能变化量相同,选项B正确;子弹在每个水球中受力是相同的,运动的时间不同,冲量I=Ft,可知每个水球对子弹的冲量不同,选项D错误.
∶2,所以子弹在每个水球中运动的时间不同,子弹在水球中沿水平方向做匀变速直线运动,则子弹在每个水球中加速度相同,受力相同,由Δv=at及子弹在每个水球中运动的时间不同可知,子弹在每个水球中速度的变化量不同,选项A、C错误;子弹在每个水球中受力是相同的,运动的位移相同,所以子弹受到的阻力对子弹做的功相等,根据动能定理ΔEk=W=Fd,可知子弹在每个水球中的动能变化量相同,选项B正确;子弹在每个水球中受力是相同的,运动的时间不同,冲量I=Ft,可知每个水球对子弹的冲量不同,选项D错误.
由题图可知,两物体匀减速运动的加速度大小相等,根据牛顿第二定律,匀减速运动过程中有Ff=ma,则摩擦力大小相等.对全过程应用动量定理,有I-Fft=0,则I1=Ff·3t0,I2=Ff·5t0,故I1∶I2=3∶5;对全过程运用动能定理得:W-Ffx=0,得W=Ffx,v-t图线与时间轴所围成的面积表示物体运动的位移,则位移之比为6∶5,整个运动过程中F1和F2做功之比为W1∶W2=x1∶x2=6∶5,故C正确.
12. 根据平衡条件可得直升机悬停时受到的升力大小为mg,故A错误;Δt时间内被螺旋桨推动的空气的质量为Δm′=ρSvΔt,螺旋桨对空气的作用力大小F= ,Δp=Δm′v,由牛顿第三定律知空气对螺旋桨的作用力大小F′=F,为使飞机向上匀速运动,有F′=mg+f,联立解得v=
,Δp=Δm′v,由牛顿第三定律知空气对螺旋桨的作用力大小F′=F,为使飞机向上匀速运动,有F′=mg+f,联立解得v= ,1 s内被螺旋桨推动的空气质量为M=ρSv=ρS
,1 s内被螺旋桨推动的空气质量为M=ρSv=ρS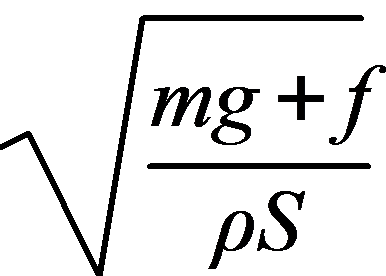 =
= ,故B错误,C正确;由动能定理可得1 s内发动机所做的功为W=
,故B错误,C正确;由动能定理可得1 s内发动机所做的功为W= Mv2=
Mv2=
 ,故D错误.
,故D错误.
1.
解法一 用动量定理,分段求解.
选物体为研究对象,对于撤去F前物体做匀加速运动的过程,始态速度为零,终态速度为v.取水平力F的方向为正方向,根据动量定理有(F-μmg)t1=mv-0,
对于撤去F后物体做匀减速运动的过程,始态速度为v,终态速度为零.根据动量定理有-μmgt2=0-mv.
联立解得t2= t1=
t1= ×6 s=12 s.
×6 s=12 s.
解法二 用动量定理,研究全过程.
选物体作为研究对象,研究整个运动过程,这个过程的始、末状态物体的速度都等于零.
取水平力F的方向为正方向,根据动量定理得
(F-μmg)t1+(-μmg)t2=0
解得t2=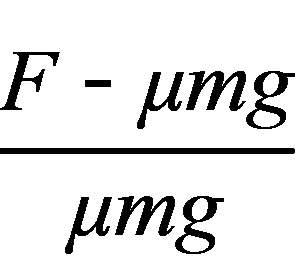 t1=
t1= ×6 s=12 s.
×6 s=12 s.
第二张
多选题
1.
以小孩运动方向为正方向,对小孩和滑板组成的系统,由动量守恒定律有0=Mv-mv′,解得滑板的速度大小v′= .
.
在小车与木块直接碰撞的瞬间,彼此作用力很大,所以它们的速度在瞬间发生改变,在此期间它们的位移可看成为零,而摆球并没有直接与木块发生力的作用,因为在它与小车共同匀速运动时,摆线沿竖直方向,因此绳的拉力不能改变小球速度的大小,即小球的速度不变,A、D错误;而小车和木块碰撞后,可能以不同的速度继续向前运动,也可能以共同速度(完全非弹性碰撞)向前运动,且小车和木块组成的系统动量守恒,B错误,C正确.
两小车及弹簧系统所受合力为零,动量守恒,以水平向右为正方向,根据动量守恒定律得m2v2-m1v1=0,解得v1∶v2=1∶2,A正确;由动量守恒定律知,弹簧弹开后左右两小车的动量大小相等,B错误;弹簧弹开过程中,左右两小车受到的弹力大小相等,作用时间相同,由I=Ft知,左右两小车受到的冲量大小之比为1∶1,C错误;由动能定理得,弹簧弹开过程弹力对左右两小车做功之比为W1∶W2= ∶
∶ =1∶2,D错误.
=1∶2,D错误.
由题图乙可知撞前vA=4 m/s,vB=0,撞后v= m/s=1
m/s=1
m/s,则由mAvA=(mA+mB)v可得mB= =3
=3
kg,A、B错误;对B有Ft=mBv-0,解得F=300 N,C正确,D错误.
设火箭的质量为m1,燃气的质量为m2.由题意可知,燃气喷出后的瞬间,燃气的动量大小p2=m2v2=50×10-3×600
kg·m/s=30
kg·m/s.以火箭运动的方向为正方向,根据动量守恒定律可得,0=m1v1-m2v2,则火箭的动量大小为p1=m1v1=m2v2=30
kg·m/s,所以A正确,B、C、D错误.
人与a、b组成的系统水平方向不受外力,设水平向右的方向为正方向,根据动量守恒,则有0=(m人+ma)va-mbvb,得 =
= <1,则a车的速率小于b车的速率;人对两车的冲量大小:Ia=mava,Ib=mbvb=(ma+m人)va>mava,结合牛顿第三定律可知,a车对人的冲量小于b车对人的冲量,故选D.
<1,则a车的速率小于b车的速率;人对两车的冲量大小:Ia=mava,Ib=mbvb=(ma+m人)va>mava,结合牛顿第三定律可知,a车对人的冲量小于b车对人的冲量,故选D.
B下落h时的速度为vB=
物块B与A碰撞过程动量守恒,则mvB=(M+m)v
以向下为正方向,则两木块从碰撞后瞬间到到达最低点过程中由动量定理有(M+m)gt-I1=0-(M+m)v
从两木块发生碰撞到木块A第一次回到初始位置的过程中弹簧对木块A的冲量I的大小为I=2I1
联立解得I=2m +2(M+m)gt
+2(M+m)gt
故选D.
8. 红壶碰撞前后的速度分别为1.2
m/s、0.3 m/s,所以红壶碰撞前后速度大小变化了0.9 m/s,故A错误;碰撞后蓝壶的加速度大小等于红壶的加速度大小,为a= =
= m/s2=0.3
m/s2=0.3
m/s2,故B正确;设碰后蓝壶的速度为v,碰前红壶的速度v0=1.2 m/s,碰后速度为v0′=0.3
m/s,根据动量守恒定律可得:mv0=mv0′+mv,解得:v=0.9
m/s,故蓝壶运动时间为t= =3
=3
s,故C错误;碰撞后两壶相距的最远距离等于碰后两图线与时间轴所围面积之差,为s=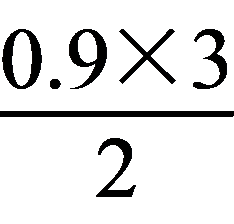 m-
m- m=1.2 m,故D错误.
m=1.2 m,故D错误.
1.
(1)设B车的质量为mB,碰后加速度大小为aB.根据牛顿第二定律有
μmBg=mBaB①
式中μ是汽车与路面间的动摩擦因数.
设碰撞后瞬间B车速度的大小为vB′,碰撞后滑行的距离为sB.由运动学公式有
vB′2=2aBsB②
联立①②式并利用题给数据得
vB′=3.0 m/s③
(2)设A车的质量为mA,碰后加速度大小为aA,根据牛顿第二定律有
μmAg=mAaA④
设碰撞后瞬间A车速度的大小为vA′,碰撞后滑行的距离为sA,由运动学公式有
vA′2=2aAsA⑤
设碰撞前的瞬间A车速度的大小为vA.两车在碰撞过程中动量守恒,有
mAvA=mAvA′+mBvB′⑥
联立③④⑤⑥式并利用题给数据得
vA≈4.3 m/s.
人跳到乙车上后,如果两车同向,且甲车的速度等于乙车的速度就可以恰好避免两车相撞
以人、甲车、乙车组成的系统为研究对象,以向右为正方向
由水平方向动量守恒得
(m1+M)v-m2v0=(m1+m2+M)v′
解得v′=1 m/s
以人与甲车为一系统,人跳离甲车过程水平方向动量守恒,得(m1+M)v=m1v′+Mu
解得u=3.8 m/s
因此,只要人跳离甲车的速度大于或等于3.8
m/s,就可避免两车相撞.
(1)物块恰好通过C点,有mg=m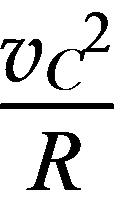
解得vC= m/s
m/s
由动能定理得,W-μmgL0= mv
mv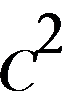
解得W=5.5 J
(2)物块由C运动到D,由动能定理得2mgR= mv
mv -
- mv
mv
解得vD=5 m/s
在D点,F-mg=m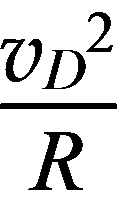
解得F=60 N
(3)若物块与木板能共速,由动量守恒定律得
mvD=(M+m)v共
解得v共=1 m/s
对物块,-μmg·x物= mv
mv -
- mv
mv ,得x物=2.4 m
,得x物=2.4 m
对木板,μmg·x板= Mv
Mv ,得x板=0.4 m,
,得x板=0.4 m,
(L+x板>x物)
(用牛顿运动定律解答同样得分)
①若s≥0.4
m,物块能和木板共速,
则由能量守恒得:Ek= mv
mv -μmg(L+x板-x物)=0.25 J
-μmg(L+x板-x物)=0.25 J
②若s<0.4
m,物块不能和木板共速,
则由能量守恒得:Ek=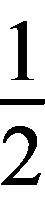 mv
mv -μmg·(L+s)=2.25-5s.
-μmg·(L+s)=2.25-5s.
第三张
多选题
1.
摆球做简谐运动,在平衡位置处位移为零,在摆角增大的过程中,摆球的位移增大,速度减小,选项A、B错误;在摆角增大的过程中,摆球受到的回复力增大,选项C正确;单摆做简谐运动,机械能守恒,所以在摆角增大的过程中,摆球机械能保持不变,选项D错误.
在振子由O到a的过程中,其位移不断增大,回复力增大,加速度增大,但是由于加速度与速度方向相反,故速度减小,选项C正确.
3.开始计时时,弹簧振子从正向最大位移处开始运动,故振动图象为A图.
4. 由题图乙可知,t=0.2
s时,振动物体远离平衡位置向右运动,位移增大,根据F=-kx可知,回复力方向向左,故加速度方向向左,A正确;t=0.6
s时,振动物体靠近平衡位置向左运动,故振动物体的速度方向向左,B错误;在t=0.4 s到t=0.8
s时间内,振动物体向平衡位置运动,速度逐渐增大,动能逐渐增大,C错误;在t=0到t=2.4 s时间内,振动物体通过的路程是4A× =60 cm,故D错误.
=60 cm,故D错误.
如果在t1时刻物块位于O点上方且向下运动,t2时刻物块位于O点下方且与t1时刻物块速度相同,则t2-t1的最小值小于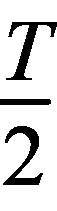 ,选项A错误;如果在t2时刻物块的动能也为Ek,则t2时刻物块速度与t1时刻大小相等,方向可能相同,也可能相反,t2-t1的最小值小于
,选项A错误;如果在t2时刻物块的动能也为Ek,则t2时刻物块速度与t1时刻大小相等,方向可能相同,也可能相反,t2-t1的最小值小于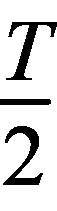 ,选项B错误;题图中O点是平衡位置,物块通过O点时位移最小,根据a=-
,选项B错误;题图中O点是平衡位置,物块通过O点时位移最小,根据a=- 知,其加速度最小,选项C正确;C、D两点关于平衡位置对称,加速度等大反向,选项D错误.
知,其加速度最小,选项C正确;C、D两点关于平衡位置对称,加速度等大反向,选项D错误.
如图甲所示,设O为平衡位置,OB(OC)代表振幅,若振子一开始从平衡位置向点C运动,振子从O→C所需时间为 .因为简谐运动具有对称性,所以振子从M→C所用时间和从C→M所用时间相等,故
.因为简谐运动具有对称性,所以振子从M→C所用时间和从C→M所用时间相等,故 =0.3 s+
=0.3 s+ s=0.4 s,解得T=1.6
s;如图乙所示,若振子一开始从平衡位置向点B运动,设点M′与点M关于点O对称,则振子从点M′经过点B到点M′所用的时间与振子从点M经过点C到点M所需时间相等,即0.2
s.振子从点O到点M′、从点M′到点O及从点O到点M所需时间相等,为
s=0.4 s,解得T=1.6
s;如图乙所示,若振子一开始从平衡位置向点B运动,设点M′与点M关于点O对称,则振子从点M′经过点B到点M′所用的时间与振子从点M经过点C到点M所需时间相等,即0.2
s.振子从点O到点M′、从点M′到点O及从点O到点M所需时间相等,为 =
= s,故周期为T=0.5 s+
s,故周期为T=0.5 s+ s≈0.53 s,故C正确.
s≈0.53 s,故C正确.

做受迫振动的物体的频率等于驱动力的频率,单摆振动时的频率由驱动力的频率决定,与单摆的固有频率无关,当驱动力频率等于单摆的固有频率时,单摆的振幅最大,发生共振,选项A错误;由题图可知,甲、乙两个单摆的固有频率之比为1∶2,则由T=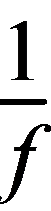 =2π
=2π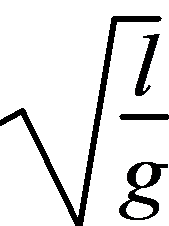 可知,l=
可知,l= ,则若两单摆放在同一地点,则甲、乙两单摆的摆长之比为4∶1;若两单摆摆长相同放在不同的地点,则甲、乙两单摆所处两地的重力加速度之比为1∶4,选项B正确,C错误;在地面附近,秒摆的摆长为l=
,则若两单摆放在同一地点,则甲、乙两单摆的摆长之比为4∶1;若两单摆摆长相同放在不同的地点,则甲、乙两单摆所处两地的重力加速度之比为1∶4,选项B正确,C错误;在地面附近,秒摆的摆长为l= ≈1 m,选项D错误.
≈1 m,选项D错误.
由单摆的周期公式T=2π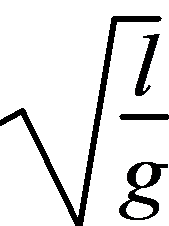 可知,小球在钉子右侧时的振动周期为在钉子左侧时振动周期的2倍,故B、D项错误;由机械能守恒定律可知,小球在左、右最大位移处距离最低点的高度相同,但由于摆长不同,所以小球在左、右两侧摆动时相对平衡位置的最大水平位移不同,当小球在钉子右侧摆动时,最大水平位移较大,故A项正确,C项错误.
可知,小球在钉子右侧时的振动周期为在钉子左侧时振动周期的2倍,故B、D项错误;由机械能守恒定律可知,小球在左、右最大位移处距离最低点的高度相同,但由于摆长不同,所以小球在左、右两侧摆动时相对平衡位置的最大水平位移不同,当小球在钉子右侧摆动时,最大水平位移较大,故A项正确,C项错误.
1.
(1)单摆的周期T= ,由单摆周期公式T=2π
,由单摆周期公式T=2π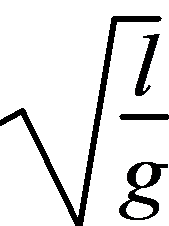 得重力加速度g=
得重力加速度g= =
= .
.
(2)为了便于测量周期和减小空气阻力,摆线选择较细且结实的线,故选A;为了减小空气阻力的影响,摆球选择质量大体积小的,故选C.
(3)为了避免运动过程中摆长发生变化,悬点要固定,不能松动,则选图乙.
(4)这样做的目的是便于调节摆长,把摆线夹得更紧一些,使摆动过程中摆长不变,因此A、C正确.
(5)摆球的直径为d=12.0 mm.
(6)摆长等于摆线的长度加上摆球的半径,A错误;将停表测量摆球完成一次全振动所用时间作为单摆的周期,误差较大,应采用累积法测量周期,D错误.
(7)根据单摆周期公式T=2π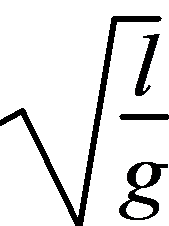 =
=
 ,所以应该作出T-
,所以应该作出T- 图像,故横坐标所代表的物理量是
图像,故横坐标所代表的物理量是 ,斜率k=
,斜率k= ,解得g=
,解得g= .
.
(8)由周期公式T=2π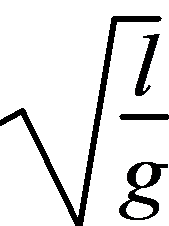 ,得g=
,得g= ,单摆振幅大小与g无关,故A错误;开始计时时,过早按下停表,周期偏大,则g偏小,故B错误;测量周期时,误将摆球(n-1)次全振动的时间记为n次全振动的时间,周期偏小,则g偏大,故C正确;摆长等于摆线的长度加上摆球的半径,若测量摆长时以悬点到小球下端边缘的距离为摆长,摆长偏大,由g=
,单摆振幅大小与g无关,故A错误;开始计时时,过早按下停表,周期偏大,则g偏小,故B错误;测量周期时,误将摆球(n-1)次全振动的时间记为n次全振动的时间,周期偏小,则g偏大,故C正确;摆长等于摆线的长度加上摆球的半径,若测量摆长时以悬点到小球下端边缘的距离为摆长,摆长偏大,由g= ,所以g偏大,故D正确.
,所以g偏大,故D正确.
(1)根据题图(b)的信息可得,摆球第一次摆到最低点时,力传感器显示的力最大,所对应的时刻为t=0.5 s.根据题图(b)的信息可得,单摆周期T=1.6
s,由单摆周期公式T=2π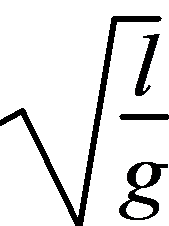 ,解得摆长为l=0.64 m.
,解得摆长为l=0.64 m.
(2)单摆振动的回复力是摆球重力在垂直摆线方向上的分力,而摆球所受重力和摆线对摆球拉力的合力在径向上提供向心力,选项B正确.
(3)测得摆长应为l+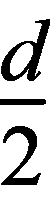 ,选项B错误;若让小球在水平面内做圆周运动,则为圆锥摆运动,测得的摆动周期不是单摆运动周期,选项D错误.
,选项B错误;若让小球在水平面内做圆周运动,则为圆锥摆运动,测得的摆动周期不是单摆运动周期,选项D错误.
第四张
多选题
1.
不能发生明显衍射的原因是障碍物的长度远大于波长,则增大波长或减小障碍物的长度可能使波发生较为明显的衍射,选项C、D错误;由λ= 知,v不变,减小f,λ增大,选项A错误,B正确.
知,v不变,减小f,λ增大,选项A错误,B正确.
质点P向动能增大的方向运动,则t= 时刻,质点P向平衡位置运动,即运动方向向下,可得该波沿x轴负方向传播,故A错误;t=
时刻,质点P向平衡位置运动,即运动方向向下,可得该波沿x轴负方向传播,故A错误;t= 时刻Q点位于波谷,速度为0,小于质点P的速度,故B错误;t=
时刻Q点位于波谷,速度为0,小于质点P的速度,故B错误;t=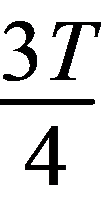 时刻,Q点位于波峰,P点在平衡位置下方且向y轴正方向运动,故C错误,D正确.
时刻,Q点位于波峰,P点在平衡位置下方且向y轴正方向运动,故C错误,D正确.
由题图乙可知,t=2 s时质点P向上振动,根据“微平移法”,结合题图甲可知波沿x轴正方向传播,A错误;根据振动图像可知,波的周期为T=4 s,根据波形图可知,波长λ=4 m,所以波速v= =1 m/s,B正确;t=2 s时刻,质点P位于平衡位置处,再经0.5 s=
=1 m/s,B正确;t=2 s时刻,质点P位于平衡位置处,再经0.5 s= T,质点P通过的路程s>
T,质点P通过的路程s> =0.05 m,C错误;Δt=1.5 s,Δx=vΔt=1.5 m=PQ,根据波的传播方向可知t=3.5 s时刻,质点Q经过平衡位置,D错误.
=0.05 m,C错误;Δt=1.5 s,Δx=vΔt=1.5 m=PQ,根据波的传播方向可知t=3.5 s时刻,质点Q经过平衡位置,D错误.
A、B两点为振动加强点,两点振幅均为2 cm,两点高度差为4 cm,故A错误;C点为B、D两点连线的中点,所以C点处在平衡位置,根据“上下坡”法,C点正向上运动,故B错误;F点为振动减弱点,它到两波源的路程之差应为半波长的奇数倍,故C错误;因周期T= =
= s=0.4 s,经t=0.1 s=
s=0.4 s,经t=0.1 s= ,A点由波峰回到平衡位置,位移为零,故D正确.
,A点由波峰回到平衡位置,位移为零,故D正确.
由题图知质点A起振方向是向下,故波源的起振方向是向下,故A错误;从t=0时刻起到质点B第一次出现波峰的时间为t′= s=0.5 s,因T=
s=0.5 s,因T= s=
s= s,则t′=3T,质点A在此过程中经过的路程s=3×4×2 cm=24 cm,故B正确,C错误;从t=0时刻起再经过t″=
s,则t′=3T,质点A在此过程中经过的路程s=3×4×2 cm=24 cm,故B正确,C错误;从t=0时刻起再经过t″= s=0.375 s时间质点B开始起振,故D错误.
s=0.375 s时间质点B开始起振,故D错误.
由振动图像可知,周期T=1×10-5 s,由波形图可知波长λ=1.5×10-2 m,则v=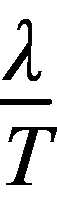 =
= m/s=1.5×103 m/s,鱼群与渔船的距离x=
m/s=1.5×103 m/s,鱼群与渔船的距离x= vt=
vt= ×1.5×103×2 m=1 500 m,故C正确,A、B、D错误.
×1.5×103×2 m=1 500 m,故C正确,A、B、D错误.
8. C
9.
由题图乙可知,t=1 s时,x=3 m处质点正在向上运动,所以波的传播方向为x轴负方向,故A错误;由题图甲知λ=4 m,由题图乙知T=2 s,则v= =2 m/s,故B错误;a、b间距离xab=(2.5-0.5) m=2 m,可知a、b相距半个波长,故此两点的速度、加速度均等大反向,故C正确;从t=1 s到t=1.5 s,质点a经过
=2 m/s,故B错误;a、b间距离xab=(2.5-0.5) m=2 m,可知a、b相距半个波长,故此两点的速度、加速度均等大反向,故C正确;从t=1 s到t=1.5 s,质点a经过 个周期,越靠近平衡位置时的速度越大,即s>10 cm,故D错误.
个周期,越靠近平衡位置时的速度越大,即s>10 cm,故D错误.
若波沿-x方向传播,则t=0.5 s=(n+ )T(n=0,1,2,…),由于0.25 s<T<0.5 s,故n=1,即0.5 s=
)T(n=0,1,2,…),由于0.25 s<T<0.5 s,故n=1,即0.5 s= T,得T=
T,得T= s.由题图可知波长λ=4 m,故波速v=
s.由题图可知波长λ=4 m,故波速v= =14 m/s,在0.5 s内,x=1 m处质点M通过的路程sM′=
=14 m/s,在0.5 s内,x=1 m处质点M通过的路程sM′= ×4A=7A=14 cm,故A错误;波沿-x方向传播,t=0.1 s≠
×4A=7A=14 cm,故A错误;波沿-x方向传播,t=0.1 s≠ ,故质点M离开平衡位置的位移不为零,故D错误;若波沿+x方向传播,则t=0.5 s=(n+
,故质点M离开平衡位置的位移不为零,故D错误;若波沿+x方向传播,则t=0.5 s=(n+ )T(n=0,1,2,…);由题知n=1,解得T=0.4 s,0.5 s=
)T(n=0,1,2,…);由题知n=1,解得T=0.4 s,0.5 s= T,x=1 m处的质点M通过的路程为sM=5A=10 cm,x=2.5 m处质点N通过的路程sN>10 cm,故两质点通过的路程不相等,故C正确;由以上分析知,B错误.
T,x=1 m处的质点M通过的路程为sM=5A=10 cm,x=2.5 m处质点N通过的路程sN>10 cm,故两质点通过的路程不相等,故C正确;由以上分析知,B错误.
由两质点的振动图像可知,t=0时刻,x1=1 m处的质点处于平衡位置向下运动,x2=7 m处的质点位于波峰处,该波的传播周期为T=4 s.若该简谐横波沿x轴正方向传播,则两质点间的距离为(n+ )λ=6 m(n=0、1、2…),则λ=
)λ=6 m(n=0、1、2…),则λ= m,由波速的公式得v=
m,由波速的公式得v= =
=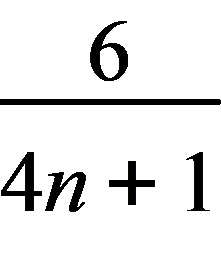 m/s(n=0、1、2…),n=0时,v=6 m/s;n=1时,v=1.2 m/s;n=2时,v=
m/s(n=0、1、2…),n=0时,v=6 m/s;n=1时,v=1.2 m/s;n=2时,v= m/s,C正确;若该简谐横波沿x轴负方向传播,则两质点间的距离为(n+
m/s,C正确;若该简谐横波沿x轴负方向传播,则两质点间的距离为(n+ )λ=6 m(n=0、1、2…),则λ=
)λ=6 m(n=0、1、2…),则λ=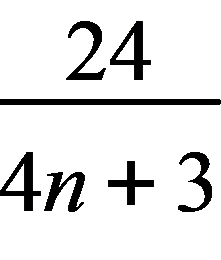 m,由波速的公式得v=
m,由波速的公式得v= =
= m/s(n=0、1、2…),n=0时,v=2 m/s;n=1时,v=
m/s(n=0、1、2…),n=0时,v=2 m/s;n=1时,v= m/s,A、B、D错误.
m/s,A、B、D错误.
1.
由题图可知,周期T=0.4 s
由于波长大于0.6 m,结合题图可知,波从A到B的传播时间Δt=0.3 s
波速v= ,代入数据得v=2 m/s,
,代入数据得v=2 m/s,
波长λ=vT,代入数据得λ=0.8 m.
2. (1)质点A第一次到达波峰,时间间隔Δt= T=0.2 s
T=0.2 s
即T=0.4 s
由v= 可知波速v=5 m/s
可知波速v=5 m/s
(2)由v= 可知,波传播到C点的时间Δt′=0.6 s,此时质点C沿y轴正方向运动,再经过0.3 s即
可知,波传播到C点的时间Δt′=0.6 s,此时质点C沿y轴正方向运动,再经过0.3 s即 T,质点C到达波谷,即y=-2 cm.
T,质点C到达波谷,即y=-2 cm.
第五张
多选题
1. A
2.
同一种介质对紫光的折射率大,而对红光的折射率小,水中入射角相同时,紫光的折射角大,所以紫光在P点下方,A错误,B正确;同理,紫光的临界角小,紫光先达到临界角发生全反射,红光后达到临界角发生全反射,C错误;根据光的反射定律,红光和紫光都发生全反射时,反射光线的传播方向一致,所以它们的反射光线射到水底时是在同一点,D错误.
3. D4. B
5.
作出光线在玻璃球体内的光路图,A、C是折射点,B是反射点,OD平行于入射光线,由几何知识得,∠AOD=∠COD=60°,则∠OAB=30°,即折射角r=30°,入射角i=60°,所以折射率n= =
= ,C正确.
,C正确.
光射入三棱镜的光路图如图所示,i1=90°-30°=60°,

由折射定律得:n=
光在BC边折射时,由折射定律有: =
=
由题意知r2=90°-30°=60°,则i2=r1
由几何关系可得r1=i2=30°,则n=
由几何知识知:从AB边上射入的光在三棱镜中的传播路程s=0.5L,
光在三棱镜中的传播速度v= =
= c,
c,
故光在三棱镜中的传播时间t= =
=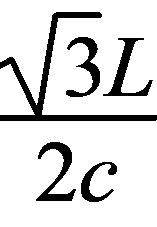 .
.
据题图乙知θ=60°时激光发生全反射,由折射定律得n= =
= ,故A错误;由速度公式得v=
,故A错误;由速度公式得v= =
= c,故B正确;θ=0°时大量的激光从O点射出,少量激光发生反射,故C错误;根据题图乙可知当θ=60°时激光发生全反射,此后θ角增大,但反射光的强度不变,故D错误.
c,故B正确;θ=0°时大量的激光从O点射出,少量激光发生反射,故C错误;根据题图乙可知当θ=60°时激光发生全反射,此后θ角增大,但反射光的强度不变,故D错误.
据题图乙知θ=60°时激光发生全反射,由折射定律得n= =
= ,故A错误;由速度公式得v=
,故A错误;由速度公式得v= =
= c,故B正确;θ=0°时大量的激光从O点射出,少量激光发生反射,故C错误;根据题图乙可知当θ=60°时激光发生全反射,此后θ角增大,但反射光的强度不变,故D错误.
c,故B正确;θ=0°时大量的激光从O点射出,少量激光发生反射,故C错误;根据题图乙可知当θ=60°时激光发生全反射,此后θ角增大,但反射光的强度不变,故D错误.
1.
光路图如图所示,

入射角θ1=60°
设折射角为θ2,由tan θ2= ,
,
得θ2=30°
根据折射定律n= ,
,
得n=1.73
2. 光束在光导纤维AB端面的入射角为θ,设折射角为α,折射光线射向侧面时的入射角为β,要保证不会有光线从侧壁射出来,则光线在侧壁发生全反射.由折射定律n=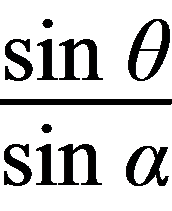
由几何关系α+β=90° sin α=cos β
恰好发生全反射的临界角公式为sin β=
得cos β=
联立得sin θ= =1
=1
即θ=90°
要保证光能从AB端面传播到另一端面,应有θ≤90°.
3. (1)如图,由题意知sin i= =
=
 sin r=
sin r=
由折射定律得n=
解得h′=1.5 m.
(2)鱼饵灯与竿梢的连线和竖直方向的夹角恰好为临界角C时,鱼饵灯发出的光恰好无法从水面BC间射出.
则有sin C=
由几何关系得sin C=
解得h″=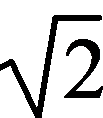 m.
m.
如图所示,

设折射角为r1,由折射定律
n= =
=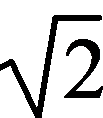
解得r1=30°
根据sin C= 可知临界角C=45°.
可知临界角C=45°.
设折射光线与AB边的交点为E,由几何知识可知在AB边的入射角为60°,大于临界角,发生全反射,反射光线与BC边平行,最终垂直于AC边射出,光在棱镜中的路程
s=b-asin 30°+a
光在棱镜中的速度v=
光从进入棱镜到它第一次射入真空所经历的时间t=
联立解得t= .
.
第六张
多选题
1.
选项A是双缝干涉,选项B是薄膜干涉,选项C是光的色散,选项D是薄膜干涉.故选C.
2. D3. D
4. B
5.
超声波的频率较大,波长较小,所以人耳能听见的声波比超声波更易发生衍射,选项A错误;光的色散现象是由光的折射引起的,选项B错误;根据麦克斯韦的电磁场理论,周期性变化的电场周围才可以产生电磁波,选项C错误;光导纤维丝内芯材料的折射率比外套材料的折射率大,选项D正确.
6.由题图中给出的甲、乙两种图样可知,甲是单缝衍射的图样,乙是双缝干涉的图样,A项正确,B、C、D项错误.
7. 由题图可知b光的折射程度较大,可知水对b光的折射率较大,根据sin C= 可知,从同种介质中斜射入空气发生全反射时,b光的临界角小于a光的临界角,选项A错误;根据v=
可知,从同种介质中斜射入空气发生全反射时,b光的临界角小于a光的临界角,选项A错误;根据v= 可知,在同种介质中传播,a光传播速度大于b光传播速度,选项B错误;b光的折射率较大,则b光波长较短,根据Δx=
可知,在同种介质中传播,a光传播速度大于b光传播速度,选项B错误;b光的折射率较大,则b光波长较短,根据Δx= λ可知,相同条件的双缝干涉实验中,b光的相邻亮条纹间距比a光的相邻亮条纹间距小,选项C错误;b光波长较短,则通过同一狭缝,a光的衍射现象比b光的衍射现象更明显,选项D正确.
λ可知,相同条件的双缝干涉实验中,b光的相邻亮条纹间距比a光的相邻亮条纹间距小,选项C错误;b光波长较短,则通过同一狭缝,a光的衍射现象比b光的衍射现象更明显,选项D正确.
单色光a的入射角为i=60°,由几何知识可知折射角为r=30°,则该棱镜对单色光a的折射率n=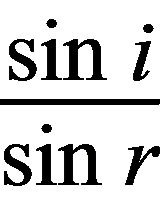 =
=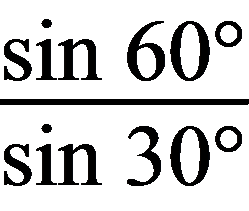 =
= ,选项A错误;在棱镜中传播,a光的折射率较大,由v=
,选项A错误;在棱镜中传播,a光的折射率较大,由v= 可知,a光的传播速度较小,选项B错误;a光的折射率大于b光的折射率,则a光的频率一定大于b光的频率,选项C正确;a光的频率大于b光的频率,则a光的波长小于b光的波长,根据Δx=
可知,a光的传播速度较小,选项B错误;a光的折射率大于b光的折射率,则a光的频率一定大于b光的频率,选项C正确;a光的频率大于b光的频率,则a光的波长小于b光的波长,根据Δx=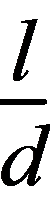 λ可知,分别通过同一双缝干涉装置,a光的相邻亮条纹间距小,选项D错误.
λ可知,分别通过同一双缝干涉装置,a光的相邻亮条纹间距小,选项D错误.
由题意可知,单色光A照射双缝时条纹间距较小,根据Δx= λ可知单色光A的波长较小,频率较大,选项A、B、C错误;因单色光B的波长较大,则用单色光A和B在同一单缝衍射的装置上做实验,在缝宽不变的情况下,单色光B更容易发生明显衍射,选项D正确.
λ可知单色光A的波长较小,频率较大,选项A、B、C错误;因单色光B的波长较大,则用单色光A和B在同一单缝衍射的装置上做实验,在缝宽不变的情况下,单色光B更容易发生明显衍射,选项D正确.
由题意可知,单色光A照射双缝时条纹间距较小,根据Δx= λ可知单色光A的波长较小,频率较大,选项A、B、C错误;因单色光B的波长较大,则用单色光A和B在同一单缝衍射的装置上做实验,在缝宽不变的情况下,单色光B更容易发生明显衍射,选项D正确.
λ可知单色光A的波长较小,频率较大,选项A、B、C错误;因单色光B的波长较大,则用单色光A和B在同一单缝衍射的装置上做实验,在缝宽不变的情况下,单色光B更容易发生明显衍射,选项D正确.
远离中心点处亮环的分布较密,故A错误;用白光照射时,仍然会出现干涉形成的圆环,故B错误;这些亮暗圆环是透镜曲面上反射光与玻璃平面上的反射光干涉形成的,故C错误;与同一亮环相对应的空气薄膜的厚度是相同的,故D正确.
12. 双缝干涉的图样是明暗相间的干涉条纹,所有条纹宽度相同且等间距,因此第一个和第三个是双缝干涉图样,根据双缝干涉条纹间距Δx= λ可知,波长越大,Δx越大,因此第一个是红光,第三个是蓝光.单缝衍射条纹是中间明亮且宽大,越向两侧宽度越小越暗,而波长越长,中间亮条纹越宽,因此第二个和第四个是单缝衍射图样,而第二个是紫光,第四个是黄光.综上所述,从左到右排列亮条纹的颜色依次是红、紫、蓝、黄,故A、C、D错误,B正确.
λ可知,波长越大,Δx越大,因此第一个是红光,第三个是蓝光.单缝衍射条纹是中间明亮且宽大,越向两侧宽度越小越暗,而波长越长,中间亮条纹越宽,因此第二个和第四个是单缝衍射图样,而第二个是紫光,第四个是黄光.综上所述,从左到右排列亮条纹的颜色依次是红、紫、蓝、黄,故A、C、D错误,B正确.
根据光发生明显衍射的条件,雾霾天气时,只有波长较长、频率较小的一部分光发生衍射绕过空气中的颗粒物到达地面,选项A、C、D错误,B正确.
14.发现光有强弱变化说明水面上反射的阳光是偏振光,而阳光本身是自然光,在反射时发生了偏振,当偏振片的方向与光的偏振方向平行时,通过的光最强,而当偏振片的方向与光的偏振方向垂直时,通过的光最弱,因此镜片起到检偏器的作用,故选B.
15. C16.
任何电磁波在真空中的传播速度均为光速,传播速度相同,A错误;电磁波均为横波,B错误;5G信号的频率更高,则其粒子性更显著,C正确;因5G信号的频率更高,则波长更小,故4G信号更容易发生明显的衍射现象,D错误.
17.所有物体都会辐射出红外线,故A、B错误;红外体温计是依据人体发射红外线来测体温的,且人体温度越高,辐射的红外线强度越大,故C错误,D正确.
填空题1.
从两狭缝发出的光,它们的频率相同,在波峰与波谷相遇的区域中,振动相互抵消,会出现暗条纹,即在C点出现暗条纹.
第七张
多选题
1.
a= 是牛顿第二定律的表达式,表明加速度与所受的合力成正比,与质量成反比,a=
是牛顿第二定律的表达式,表明加速度与所受的合力成正比,与质量成反比,a= 不属于比值定义法,故A错误;公式P=
不属于比值定义法,故A错误;公式P= 是纯电阻电路中求解电功率的变形公式,不属于比值定义法,故B错误;电场强度是电荷在电场中所受的电场力与其电荷量的比值,是用比值定义法定义的,故C正确;公式I=
是纯电阻电路中求解电功率的变形公式,不属于比值定义法,故B错误;电场强度是电荷在电场中所受的电场力与其电荷量的比值,是用比值定义法定义的,故C正确;公式I= 是欧姆定律的数学表达式,表明导体中的电流与导体两端的电压成正比,与这段导体的电阻成反比,不属于比值定义法,故D错误.
是欧姆定律的数学表达式,表明导体中的电流与导体两端的电压成正比,与这段导体的电阻成反比,不属于比值定义法,故D错误.
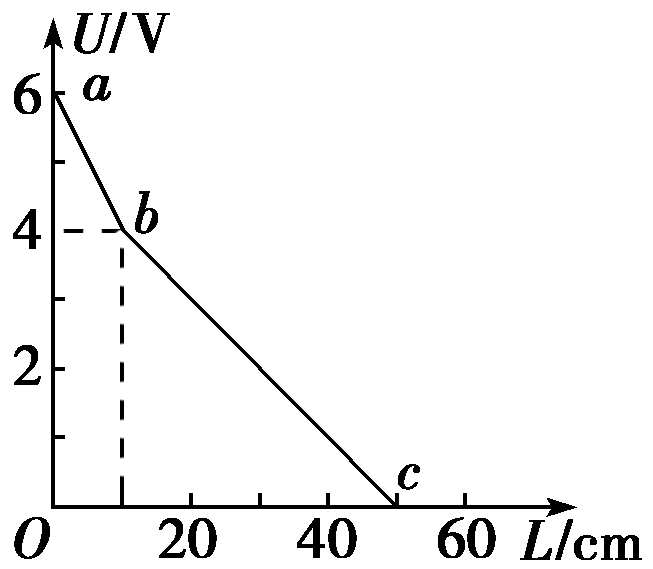
两导线串联,电流相等,I1=I2,从两段图线上截取相同的电压,ΔU1=ΔU2,保证电阻是相等的,此时长度之比为L1∶L2=1∶2,由电阻定律知,横截面积之比等于长度之比,S1∶S2=1∶2,B正确,A、C、D错误.
3.当R4处出现火情时,R4↓→R总↓→I总↑→U外↓→U并↓→IR3↓⇒I↑,故A项正确.
4.电源的外电压与电流的关系为U=E-Ir=1.5-0.75I,作电源的外电压与电流的关系图线,交点所对应的电压U=0.75 V,电流I=1 A,则灯泡的实际功率P=UI=0.75 W,电源的总功率P总=EI=1.5 W,故D正确,A、B、C错误.
5.若L1灯泡断路,则L1不亮,A1不会有示数,这和题目已知条件矛盾,因此A错误;若L2断路,则A1不会有示数,故B错误;若L2短路,由于L2和A1支路无电阻,并联电路两端电压为零,所以A2和L3支路无电流,灯L1亮,C正确;若L3短路,则A2应有示数,A1无示数,故D错误.
6.由I= 可知,待测电阻的电阻值越小,I越大,多用电表的指针偏角越大,故A正确;测量电路中的某个电阻,应该把该电阻与电路断开,故B错误;测量电阻时如果指针偏转过大,所选挡位太大,应换小挡,应将选择开关拨至倍率较小的挡位,重新调零后测量,故C错误;用同一挡位测量阻值不同的电阻时不必重新调零,换挡后要重新进行欧姆调零,故D错误.
可知,待测电阻的电阻值越小,I越大,多用电表的指针偏角越大,故A正确;测量电路中的某个电阻,应该把该电阻与电路断开,故B错误;测量电阻时如果指针偏转过大,所选挡位太大,应换小挡,应将选择开关拨至倍率较小的挡位,重新调零后测量,故C错误;用同一挡位测量阻值不同的电阻时不必重新调零,换挡后要重新进行欧姆调零,故D错误.
把电流计改装成0.6 A的电流表需要并联一个分流电阻,分流电阻阻值:R= =
=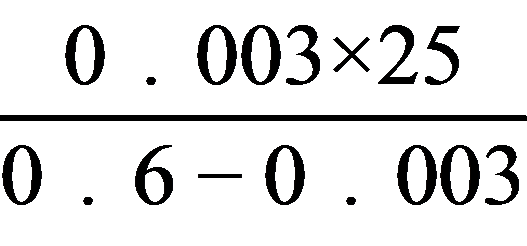 Ω≈0.126 Ω,故A正确,B错误;把电流计改装成3 V的电压表需要串联分压电阻,串联电阻阻值:R′=
Ω≈0.126 Ω,故A正确,B错误;把电流计改装成3 V的电压表需要串联分压电阻,串联电阻阻值:R′=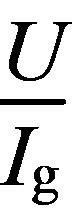 -Rg=
-Rg= Ω=975 Ω,故C错误,D正确.
Ω=975 Ω,故C错误,D正确.
当油面下降时,浮标位置降低,在杠杆作用下,滑动变阻器的滑片O向上移动,滑动变阻器连入电路的阻值变大,根据I= 可知电路中的电流变小,电流表示数变小,故选项A、C错误;B、D正确.
可知电路中的电流变小,电流表示数变小,故选项A、C错误;B、D正确.
1.
(1)二极管具有单向导电性,而欧姆表中指针偏转较大说明电阻较小,即为正向电流;而欧姆表内部的电源正极接在黑表笔上,故黑表笔接在二极管的正极处电流较大,故由题意可知,二极管左侧为正.
(2)由图示表盘可知,欧姆表示数为:22×1 kΩ=22 kΩ,由图示表盘可知,指针指在中央刻度线附近,不需要重新换挡测量.
(3)①由题意可知,采用的电源电压为3 V,故为了安全和准确,电压表应选取D,3 V的量程;该二极管允许通过的最大电流为50 mA,故电流表应选F.
②由题意可知,本实验要求作出伏安特性曲线,故要求多测数据,故应采用分压接法;同时,因二极管正向接入时电阻较小,故应采用电流表外接法;其实验的原理图如图甲,然后依次连接实验的电路图如图乙.
2.(1)灯L的电阻为:RL= =
= Ω=12 Ω
Ω=12 Ω
当P滑到下端时,R2被短路,灯L与整个变阻器R并联,此时灯正常发光,通过灯L的电流为:
IL= =
= A=0.5 A.
A=0.5 A.
通过变阻器R的电流为:
IR=IA-IL=1 A-0.5 A=0.5 A.
则IR=IL即得滑动变阻器最大值为:R=RL=12 Ω.
(2)电源电动势:
E=I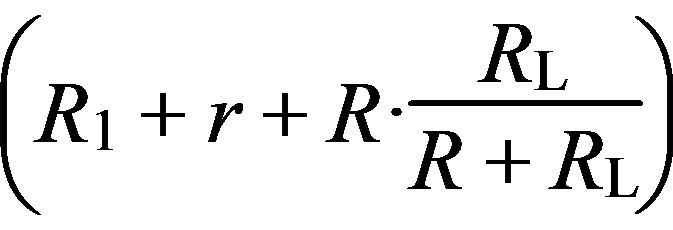 =1×(4+2+6)V=12 V
=1×(4+2+6)V=12 V
当P滑到上端时,灯L、变阻器R及电阻R2都被短路,此时的电流表的读数为:
I′= =
= A=2 A.
A=2 A.
(3)P位于变阻器的中点时,灯L与 并联后再与R1串联.此时:R并=4 Ω
并联后再与R1串联.此时:R并=4 Ω
总电流为:I总= =
= A=1.2 A.
A=1.2 A.
并联部分的电压为:U并=I总·R并=1.2×4 V=4.8 V.
变阻器上消耗的功率为:PR=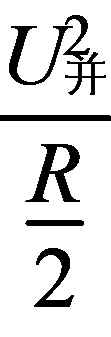 =
= W=3.84 W.
W=3.84 W.
第八张
多选题
1.
电能转化为化学能的功率为UI-I2r,充电器输出的电功率为UI,选项A正确,选项B错误;电池产生的热功率为I2r,选项C正确;充电器的充电效率为 ×100%,选项D错误.
×100%,选项D错误.
开关闭合时,电容器两板间的电压等于电阻R2两端的电压,小于电源的电动势.当开关断开时,电路稳定时,电路中没有电流,电容器板间电压等于电源的电动势,则知电容器板间电压增大,板间场强增大,液滴所受电场力增大,则液滴将向上运动.由于电容器的电压增大,由公式Q=CU可知,电容器上的带电量将增大.故选B、D.
3.由题图可知滑动变阻器的滑片由中点滑向B端时,滑动变阻器连入电路中的阻值R增大,则外电路的总阻值R总增大,干路电流I=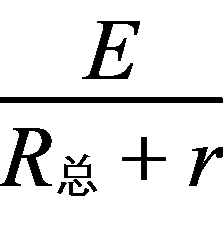 ,因R总增大,所以I减小;路端电压U=E-Ir,因I减小,所以U增大,即电压表的读数增大;R2两端的电压U2=E-I(R1+r),因I减小,所以U2增大,由I2=
,因R总增大,所以I减小;路端电压U=E-Ir,因I减小,所以U增大,即电压表的读数增大;R2两端的电压U2=E-I(R1+r),因I减小,所以U2增大,由I2= 知,I2增大,即电流表的读数增大.故选项A正确,选项B、C、D均错误.
知,I2增大,即电流表的读数增大.故选项A正确,选项B、C、D均错误.
由电路图可知,U1、U2分别测R1、R2两端的电压,电流表测通过这个电路的总电流,U3是路端电压,由欧姆定律可知R1= =
= (因R1是定值电阻),故选项A正确.U2=E-I(R1+r)(因E、R1、r均是定值),则
(因R1是定值电阻),故选项A正确.U2=E-I(R1+r)(因E、R1、r均是定值),则 =R1+r不变,故选项B错误,C正确.
=R1+r不变,故选项B错误,C正确. =R1+R2,因R2变大,则
=R1+R2,因R2变大,则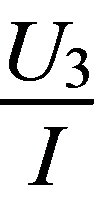 变大;又由于U3=E-Ir,可知
变大;又由于U3=E-Ir,可知 =r不变,故D正确.综上所述,正确选项为A、C、D.
=r不变,故D正确.综上所述,正确选项为A、C、D.
图线a是由路端电压与干路电流的数据所描绘的,图线b是R0的U-I图线且U2=IR0,所以A错误;由a图线得,电源内阻r=1.0 Ω,电源电动势E=1.50 V,B正确;由b图线可求出定值电阻R0=2.0 Ω,图象中两直线的交点表示此时电路中的电流为0.5 A,电压表V1的示数U1=1.0 V,电压表V2的示数U2=1.0 V,此时R0上消耗的功率P0=IU2=0.5 W,所以C错误;把E=1.50 V,r=1.0 Ω,I=0.5 A代入闭合电路欧姆定律公式E=I(R外+r)可得R外=2.0 Ω,由上述可知此时R0=2.0 Ω,所以此时滑动变阻器电阻R=0,D正确.
6.根据闭合电路的欧姆定律和U-I图象特点可知,阴影部分的面积表示负载电阻消耗的功率,即电源输出功率,A正确,B错误;当满足α=β时,电源内阻等于负载电阻,电源的效率为50%,输出功率最大,C、D错误.
混合题1.
(1)若采用限流式接法,则电路中的最小阻值R= =
= =6.7 Ω,与待测电阻Rx的阻值较接近,故电流表应选用B,电压表应选用C,实验电路应采用题图中的甲.
=6.7 Ω,与待测电阻Rx的阻值较接近,故电流表应选用B,电压表应选用C,实验电路应采用题图中的甲.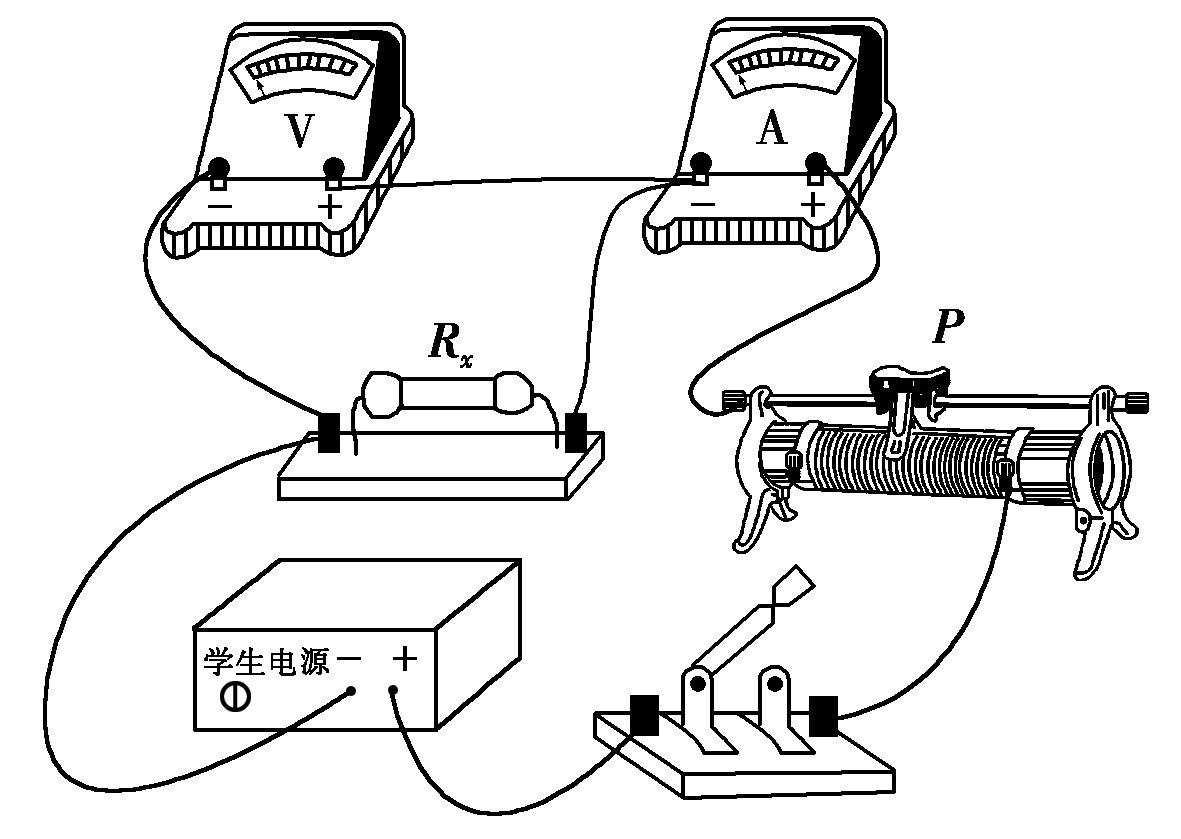
(2)实物图见答案.
(3)由题图3可得该电阻的测量值
Rx= =
=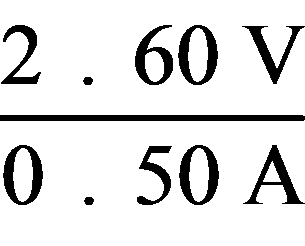 =5.2 Ω.
=5.2 Ω.
(4)若在(1)问中选用甲电路,产生误差的主要原因是电流表测量值大于流经Rx的电流值;若在(1)问中选用乙电路,产生误差的主要原因是电压表测量值大于Rx两端的电压值.
2.(1)若采用限流式接法,则电路中的最小阻值R= =
= =6.7 Ω,与待测电阻Rx的阻值较接近,故电流表应选用B,电压表应选用C,实验电路应采用题图中的甲.
=6.7 Ω,与待测电阻Rx的阻值较接近,故电流表应选用B,电压表应选用C,实验电路应采用题图中的甲.
(2)实物图见答案.
(3)由题图3可得该电阻的测量值
Rx= =
=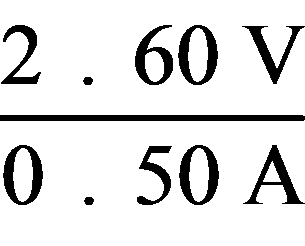 =5.2 Ω.
=5.2 Ω.
(4)若在(1)问中选用甲电路,产生误差的主要原因是电流表测量值大于流经Rx的电流值;若在(1)问中选用乙电路,产生误差的主要原因是电压表测量值大于Rx两端的电压值.
解答题1.
(1)欧姆表读数=刻度盘读数×倍率,读数是Rx=7 Ω.
(2)①由于待测电阻的阻值远小于电压表的内阻,所以电流表使用外接法,故选图2作为测量电路.
②所连实物图如图所示.
③U-I图象的斜率表示电阻的阻值,由所作的图象可知,图象的斜率为k= ≈6.25,故被测电阻的阻值为Rx=6.25 Ω.
≈6.25,故被测电阻的阻值为Rx=6.25 Ω.
(3)①在步骤A中电阻箱的读数为R1=20 Ω.
②由于R1与Rx串联在电路中所起的作用与R2相同(电压表指针指示同一位置),则有R1+Rx=R2,故有Rx=R2-R1.由题意可知R1=20 Ω,R2=26 Ω,故被测电阻的阻值为Rx=R2-R1=26 Ω-20 Ω=6 Ω.

(1)根据闭合电路的欧姆定律:I1= ;代入数据解得:r0=
;代入数据解得:r0= -R=
-R= Ω=1 Ω.
Ω=1 Ω.
(2)开关S闭合后路端电压:U=E-I2r0=(40-4.0×1) V=36 V流过R的电流强度为:IR= =1.5 A,
=1.5 A,
流过电动机的电流强度为:I=I2-IR=(4.0-1.5) A=2.5 A
电动机发热消耗的功率为:P热=I2r=(2.52×0.4) W=2.5 W电动机转化为机械能的功率:P机=UI-P热=87.5 W.
(3)开关S闭合时电源输出功率为:P=UI2=144 W电动机的机械效率:η=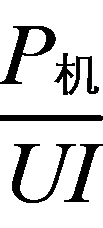 ×100%=
×100%=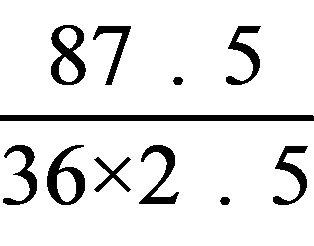 ×100%≈97.2%.
×100%≈97.2%.
第九张
多选题
1.
设三角形边长为l,通过导体棒MN的电流大小为I,则根据并联电路的规律可知通过导体棒ML和LN的电流大小为 ,如图所示,依题意有F=BlI,则导体棒ML和LN所受安培力的合力为F1=
,如图所示,依题意有F=BlI,则导体棒ML和LN所受安培力的合力为F1= BlI=
BlI= F,方向与F的方向相同,所以线框LMN受到的安培力大小为F+F1=1.5F,选项B正确.
F,方向与F的方向相同,所以线框LMN受到的安培力大小为F+F1=1.5F,选项B正确.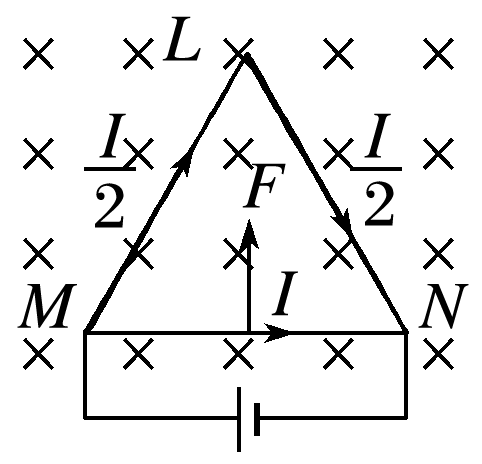
 在两导线中均通有方向垂直于纸面向里的电流I时,纸面内与两导线距离为l的a点处的磁感应强度为0,由此可知,外加的磁场方向与PQ平行,且由Q指向P,即B1=B0;依据几何关系有:BPcos 30°=
在两导线中均通有方向垂直于纸面向里的电流I时,纸面内与两导线距离为l的a点处的磁感应强度为0,由此可知,外加的磁场方向与PQ平行,且由Q指向P,即B1=B0;依据几何关系有:BPcos 30°=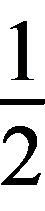 B0,解得通电导线P或Q在a处的磁场大小均为BP=
B0,解得通电导线P或Q在a处的磁场大小均为BP= B0;当P中的电流反向,其他条件不变,再依据几何关系及三角知识,则有:
B0;当P中的电流反向,其他条件不变,再依据几何关系及三角知识,则有:
B2=BP= B0,方向垂直于PQ向上,由矢量的合成法则,那么a点处磁感应强度的大小为B=
B0,方向垂直于PQ向上,由矢量的合成法则,那么a点处磁感应强度的大小为B= =
=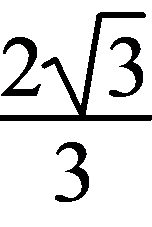 B0,故B正确,A、C、D错误.
B0,故B正确,A、C、D错误.
同向电流相互吸引,故A错误;为判断F1的方向,需要知道I2在I1处产生的磁场方向,故B错误;F1和F2是作用力和反作用力,大小相等,方向相反,故C错误;增大电流I2,F1、F2同时增大,故D正确.
4.磁场在转动的过程中,杆处于平衡状态,杆所受重力的大小和方向不变,悬线的拉力方向不变,由图 解法结合左手定则可知,在磁场沿逆时针方向缓慢转动的过程中,安培力先减小后增大,由F=BIL可知,磁场的磁感应强度先减小后增大,故选C.
解法结合左手定则可知,在磁场沿逆时针方向缓慢转动的过程中,安培力先减小后增大,由F=BIL可知,磁场的磁感应强度先减小后增大,故选C.
电流的方向与负电荷运动的方向相反,所以阴极射线管内电流的方向向左;由图可知,电子受到的洛伦兹力的方向向下,所以阴极射线管处的磁场的方向垂直于纸面向里,由安培定则可知,AB中电流的方向向左,故A错误,B正确;若要使电子束的径迹向上弯曲,则阴极射线管处的磁场的方向需向外,可以改变AB中的电流方向来实现,故C正确;由以上的分析可知,电子束的径迹与AB中的电流方向有关.故D错误.
6.由图可知,向下运动的正电荷受到的洛伦兹力的方向向右,由左手定则可知,磁场的方向垂直于纸面向里.故选B.
7.要使电荷能做直线运动,必须用电场力抵消洛伦兹力,本题正电荷受洛伦兹力的方向沿y轴正方向,故电场力必须沿y轴负方向且qE=Bqv,即E=Bv.
8.要使电荷能做直线运动,必须用电场力抵消洛伦兹力,本题正电荷受洛伦兹力的方向沿y轴正方向,故电场力必须沿y轴负方向且qE=Bqv,即E=Bv.
9.带电油滴做匀速圆周运动,重力与电场力平衡,重力向下,则电场力向上,可知带电油滴带负电,选项A正确;洛伦兹力提供向心力,故:mg=Eq,qvB=m ,由于只有E与B已知,故无法求解v和R;周期T=
,由于只有E与B已知,故无法求解v和R;周期T= =
= ,可以求解,故B正确,C、D错误.
,可以求解,故B正确,C、D错误.
由r= 得当r=R时,质子有最大速度vm=
得当r=R时,质子有最大速度vm= ,即B、R越大,vm越大,vm与加速电压无关,A对,B错.随着质子速度v的增大,质量m会发生变化,据T=
,即B、R越大,vm越大,vm与加速电压无关,A对,B错.随着质子速度v的增大,质量m会发生变化,据T= 知质子做圆周运动的周期也变化,所加交流电与其运动不再同步,即质子不可能一直被加速下去,C错.由上面周期公式知α粒子与质子做圆周运动的周期不同,故此装置不能用于加速α粒子,D错.
知质子做圆周运动的周期也变化,所加交流电与其运动不再同步,即质子不可能一直被加速下去,C错.由上面周期公式知α粒子与质子做圆周运动的周期不同,故此装置不能用于加速α粒子,D错.
因导电材料上表面的电势比下表面的低,故上表面带负电荷,根据左手定则可判断自由运动电荷带负电,则B、D两项均错误.设长方体形材料长度为L,总电荷量为Q,则其单位体积内自由运动电荷数为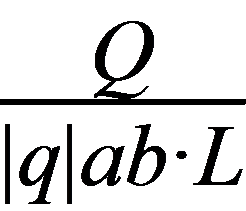 ,当电流I稳恒时,材料内的电荷所受电场力与磁场力相互平衡,则有
,当电流I稳恒时,材料内的电荷所受电场力与磁场力相互平衡,则有 =BIL,故
=BIL,故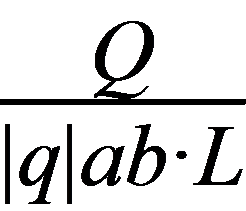 =
= ,A项错误,C项正确.
,A项错误,C项正确.
1.
(1)金属棒做匀加速直线运动,有v2=2as,
解得v=
(2)金属棒所受安培力F安=IdB
金属棒所受合力F=mgsin θ-F安
由牛顿第二定律有F=ma
解得I=
(3)金属棒的运动时间t=
通过的电荷量Q=It
解得Q= .
.
2.(1)当金属棒刚好达到向上运动的临界状态时,金属棒受到的摩擦力为最大静摩擦力,方向平行斜面向下,对金属棒受力分析,如图甲所示,此时金属棒所受安培力最大,设为F1,则有
垂直斜面方向:FN=F1sin θ+mgcos θ
沿斜面方向:F1cos θ=mgsin θ+Ffmax
又Ffmax=μFN
以上三式联立并代入数据可得F1=8 N
当金属棒刚好达到向下运动的临界状态时,金属棒受到的摩擦力为最大静摩擦力,方向平行斜面向上,其受力分析如图乙所示,此时金属棒所受安培力最小,设为F2,则有
FN′=F2sin θ+mgcos θ,
F2cos θ+Ffmax′=mgsin θ,
Ffmax′=μFN′
以上三式联立并代入数据可得F2= N
N
所以金属棒受到的安培力的取值范围为 N≤F≤8 N
N≤F≤8 N
(2)因磁场与金属棒垂直,所以金属棒受到的安培力为F=BIL,因此有I= ,由安培力的取值范围可知电流的取值范围为
,由安培力的取值范围可知电流的取值范围为 A≤I≤4 A
A≤I≤4 A
设电流为I1= A时滑动变阻器接入电路中的阻值为R1,由闭合电路欧姆定律,有E-I1r=I1(R0+R1),
A时滑动变阻器接入电路中的阻值为R1,由闭合电路欧姆定律,有E-I1r=I1(R0+R1),
代入数据可得R1=30 Ω
设电流为I2=4 A时滑动变阻器接入电路中的阻值为R2,由闭合电路欧姆定律,有E-I2r=I2(R0+R2),
代入数据可得R2=0
所以滑动变阻器接入电路中的阻值范围为0≤R≤30 Ω.
第十张
多选题
1.
根据题图中几何关系,tan 60°= ,tan 30°=
,tan 30°= ,带电粒子在匀强磁场中运动,r=
,带电粒子在匀强磁场中运动,r= ,联立解得带电粒子1的比荷与带电粒子2的比荷比值为3∶1,选项A正确,选项B错误;带电粒子1与带电粒子2在磁场中运动时间比值为
,联立解得带电粒子1的比荷与带电粒子2的比荷比值为3∶1,选项A正确,选项B错误;带电粒子1与带电粒子2在磁场中运动时间比值为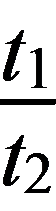 =
= =2
=2 =2∶3,选项C、D错误.
=2∶3,选项C、D错误.
①当圆环受到的洛伦兹力F洛=qvB<G=mg时,即v< 时,圆环水平方向受到向右的电场力F=qE和向左的摩擦力Ff=μ(mg-qvB),由牛顿第二定律得加速度a=
时,圆环水平方向受到向右的电场力F=qE和向左的摩擦力Ff=μ(mg-qvB),由牛顿第二定律得加速度a= ,则当Ff=0时,即mg=qvB时,加速度最大为am=
,则当Ff=0时,即mg=qvB时,加速度最大为am=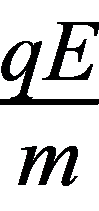 ,C正确;加速度a=
,C正确;加速度a= =
=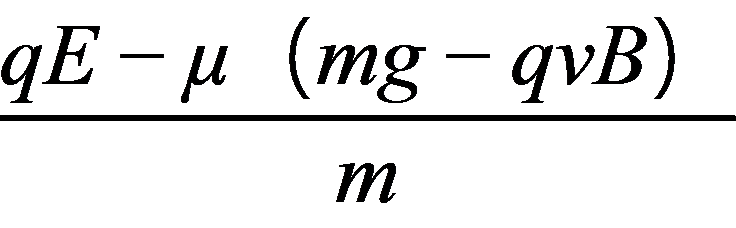 ,因为qE >μmg,圆环一开始做加速运动,但F洛=qvB逐渐增大,则摩擦力Ff=μ(mg-qvB)逐渐减小,加速度随着增大,这一阶段圆环做加速度增大的加速运动.②当圆环受到的洛伦兹力F洛=qvB>G=mg时,即v>
,因为qE >μmg,圆环一开始做加速运动,但F洛=qvB逐渐增大,则摩擦力Ff=μ(mg-qvB)逐渐减小,加速度随着增大,这一阶段圆环做加速度增大的加速运动.②当圆环受到的洛伦兹力F洛=qvB>G=mg时,即v> 时,圆环水平方向受到向右的电场力F=qE和向左的摩擦力Ff=μ(qvB-mg),由牛顿第二定律得加速度a=
时,圆环水平方向受到向右的电场力F=qE和向左的摩擦力Ff=μ(qvB-mg),由牛顿第二定律得加速度a= ,洛伦兹力F洛=qvB继续增大,则摩擦力Ff=μ(qvB-mg)逐渐增大,加速度a=
,洛伦兹力F洛=qvB继续增大,则摩擦力Ff=μ(qvB-mg)逐渐增大,加速度a= 减小,这一阶段圆环做加速度减小的加速运动,直到F=qE=Ff=μ(qvB-mg),即vm=
减小,这一阶段圆环做加速度减小的加速运动,直到F=qE=Ff=μ(qvB-mg),即vm= =
= +
+ 时,加速度减为0,之后圆环以这个速度做匀速直线运动,D错误;综合以上分析,可知带电圆环将先做加速度增大的加速运动,再做加速度减小的加速运动,最后做匀速运动,A、B错误.
时,加速度减为0,之后圆环以这个速度做匀速直线运动,D错误;综合以上分析,可知带电圆环将先做加速度增大的加速运动,再做加速度减小的加速运动,最后做匀速运动,A、B错误.
A向右偏转,根据左手定则知,A为负离子,B向左偏转,根据左手定则知,B为正离子,故A错误.离子在磁场中做圆周运动,由几何关系可得r= ,l为PQ距离,sin 60°∶sin 30°=
,l为PQ距离,sin 60°∶sin 30°= ∶1,则A、B两离子的半径之比为1∶
∶1,则A、B两离子的半径之比为1∶ ,故B正确.离子的速率v=
,故B正确.离子的速率v= ,时间相同,半径之比为1∶
,时间相同,半径之比为1∶ ,圆心角之比为2∶1,则速率之比为2∶
,圆心角之比为2∶1,则速率之比为2∶ ,故C错误.根据r=
,故C错误.根据r= 知,
知, =
= ,因为速度大小之比为2∶
,因为速度大小之比为2∶ ,半径之比为1∶
,半径之比为1∶ ,则比荷之比为2∶1,故D正确.
,则比荷之比为2∶1,故D正确.
 由于粒子比荷相同,由r=
由于粒子比荷相同,由r= 可知速度相同的粒子运动半径相同,运动轨迹也必相同,B正确.对于入射速度不同的粒子在磁场中可能的运动轨迹如图所示,由图可知,粒子的轨迹直径不超过磁场边界一半时转过的圆心角都相同,运动时间都为半个周期,而由T=
可知速度相同的粒子运动半径相同,运动轨迹也必相同,B正确.对于入射速度不同的粒子在磁场中可能的运动轨迹如图所示,由图可知,粒子的轨迹直径不超过磁场边界一半时转过的圆心角都相同,运动时间都为半个周期,而由T= 知所有粒子在磁场运动周期都相同,A、C皆错误.再由t=
知所有粒子在磁场运动周期都相同,A、C皆错误.再由t=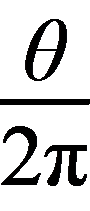 T=
T= 可知D正确.
可知D正确.
小球带负电沿逆时针方向旋转,小球所受的洛伦兹力方向背离圆心,当洛伦兹力的大小大于小球原来所受合力大小时,绳子断后,小球做顺时针的匀速圆周运动,半径变大;当洛伦兹力的大小等于小球原来所受合力大小时,半径不变;也可能洛伦兹力小于之前合力的大小,则半径减小.故A、B错误,C、D正确.
6.带电液滴受竖直向下的重力G、沿电场线方向的电场力F、垂直于速度方向的洛伦兹力F洛,由于α>β,这三个力的合力不可能沿带电液滴的速度方向,因此这三个力的合力一定为零,带电液滴做匀速直线运动,不可能做曲线运动和匀变速直线运动,故选项A、B错误.当带电液滴带正电,且电场线方向斜向上时,带电液滴受竖直向下的重力G、沿电场线向上的电场力F、垂直于速度方向斜向左上方的洛伦兹力f作用,这三个力的合力可能为零,带电液滴沿虚线L做匀速直线运动.如果带电液滴带负电或电场线方向斜向下时,带电液滴所受合力不为零,不可能沿直线运动,故选项C、D正确.
7.导体棒做平抛运动时,由于高度一定,则时间一定,设为t,则被抛出时的速度为v= ,则安培力做功为:W=
,则安培力做功为:W= mv2=
mv2= m(
m( )2;由题可知,两个导体棒落地位置与导轨右端的水平距离分别为s1和s2,而且导体棒质量相同,则安培力做功之比为:
)2;由题可知,两个导体棒落地位置与导轨右端的水平距离分别为s1和s2,而且导体棒质量相同,则安培力做功之比为: =
= ,故选项B正确,A、C、D错误.
,故选项B正确,A、C、D错误.
如图甲所示,导体棒处的磁场方向指向右上方,根据左手定则可知,导体棒受到的安培力方向垂直于磁场方向指向右下方,根据牛顿第三定律,对条形磁铁受力分析,如图乙所示,所以台秤对条形磁铁的支持力减小,即台秤示数F1>F2,在水平方向上,由于F′有水平向左的分力,条形磁铁压缩弹簧,所以弹簧长度变短.
解答题1.
粒子运动轨迹如图所示:
根据洛伦兹力公式F=qvB可知,磁感应强度一定时,粒子进入磁场的速度越大,在磁场中偏转量越小.故当磁感应强度取最大值时,若粒子恰好不飞离屏,则加速电压有最小值.设此时粒子刚好打在屏的最下端B点,根据带电粒子在磁场中运动特点可知,粒子偏离方向的夹角正切值为tan θ= ,解得:tan θ=
,解得:tan θ= ,粒子偏离方向的夹角:θ=60°=
,粒子偏离方向的夹角:θ=60°= ,
,
由几何关系可知,此时粒子在磁场中对应的回旋半径为:R=rtan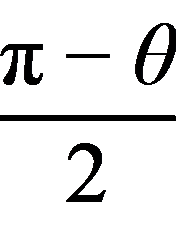 =0.1
=0.1 m ①
m ①
带电粒子在电场中加速,由动能定理得:qU= mv2 ②
mv2 ②
带电粒子在磁场中偏转时,洛伦兹力提供向心力,
由牛顿第二定律可得:qvB= ③
③
联立①②③解得:U= =60 V,
=60 V,
故加速电压的最小值为60 V.
2.(1)设粒子的初速度大小为v,粒子在极板间做匀速直线运动,则有:
qvB1=qE
设粒子在圆形区域中做匀速圆周运动的半径为r,则有:
qvB2=m
粒子速度方向偏转了60°,有
r=2Rsin 60°
解得:B2=0.1 T.
(2)撤去磁场B1后,粒子在极板间做类平抛运动,设在板间运动时间为t,运动的加速度为a,飞出电场时竖直方向的速度为vy,则有:
qE=ma
l=vt
vy=at
tan θ=
解得:tan θ= ,即θ=30°.
,即θ=30°.
(1)粒子a竖直向下穿过OC,在磁场中轨迹圆心如图甲为O1,OO1=Rcot θ,OO1=L-R
得粒子圆周运动的轨迹半径
R= L ①
L ①
由洛伦兹力提供圆周运动向心力有:
qv1B= ②
②
由①②两式解得:v1= ③
③
粒子a竖直向下穿过OC垂直进入匀强电场后,做类平抛运动,则有:
qE=ma
Rcot θ=v1t
解得t=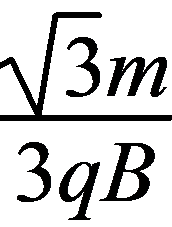
x= at2=
at2=
OP=R+x= L+
L+ .
.
(2)由qv2B=m
解得:R2= L
L
粒子在磁场中做匀速圆周运动的周期为:
T= =
=
 如图乙所示最后出磁场的粒子从OC边上的E点射出,弦ME最长为直径,ME=2R2=
如图乙所示最后出磁场的粒子从OC边上的E点射出,弦ME最长为直径,ME=2R2= L,在磁场中运动的时间为:t1=
L,在磁场中运动的时间为:t1= T=
T=
MF为垂直OC的一条弦,则MF为最短的弦,从F点射出的粒子运动时间最短,此时轨迹圆心为O2,由三角形关系得:
MF=Lsin θ= L,
L,
sin α= =
= ,
,
所以可得α=30°
此粒子的运动时间t2= T=
T=
时间差为Δt=t1-t2= .
.
第十一张
多选题
1.
电流表有示数时可判断有磁场存在,沿某方向运动而无示数不能确定磁场是否存在,只有C正确.
2. 根据E=Blv,感应电动势2Blv,A、B间的电势差U= ,C项正确.
,C项正确.
根据题设条件可知,闭合电键调节滑动变阻器R的滑动触头,使两个灯泡的亮度相同,说明此时滑动变阻器R接入电路的阻值与线圈L的电阻一样大,断开电键再重新闭合电键的瞬间,根据自感原理可判断,A2立刻变亮,而A1逐渐变亮,A、B均错误;稳定后,自感现象消失,根据题设条件可判断,线圈L和R两端的电势差一定相同,A1和A2两端的电势差也相同,所以C正确、D错误.
4.根据右手螺旋定则可知导线上方的磁场方向垂直纸面向外,下方的磁场方向垂直纸面向里,而且越靠近导线磁场越强,所以闭合导线框ABC在下降过程中,导线框内垂直于纸面向外的磁通量先增大,当BC边与导线重合时,达到最大,再向下运动,导线框内垂直于纸面向外的磁通量逐渐减小至零,然后随导线框的下降,导线框内垂直于纸面向里的磁通量增大,当达到最大,继续下降时由于导线框逐渐远离导线,使导线框内垂直于纸面向里的磁通量再逐渐减小,所以根据楞次定律可知,感应电流的磁场总是阻碍内部磁通量的变化,所以感应电流的磁场先向里,再向外,最后向里,所以导线框中感应电流的方向依次为ACBA→ABCA→ACBA,A正确;当导线框内的磁通量为零时,内部的磁通量仍然在变化,有感应电动势产生,所以感应电流不为零,B错误.根据对楞次定律的理解,感应电流的效果总是阻碍导体间的相对运动,由于导线框一直向下运动,所以导线框所受安培力的合力方向一直向上,不为零,C、D错误.
5.线圈冲入匀强磁场时,产生感应电流,线圈受安培力作用做减速运动,动能也减少.同理,线圈冲出匀强磁场时,动能减少,进、出时减少的动能都等于克服安培力做的功.由于进入时的速度大,故感应电流大,安培力大,安培力做的功也多,减少的动能也多,线圈离开磁场过程中,损失动能少于它在磁场左侧时动能的一半,因此线圈离开磁场仍继续运动.
6. 导线框进入磁场中0到L的过程中,由右手定则知,感应电流的方向为顺时针,即负方向,感应电流I= ,大小恒定,A、B不正确;导线框进入磁场中L至2L的过程中,导线框左右两侧均切割磁感线,由右手定则,可判断感应电流的方向为逆时针,即为正方向,感应电流I′=
,大小恒定,A、B不正确;导线框进入磁场中L至2L的过程中,导线框左右两侧均切割磁感线,由右手定则,可判断感应电流的方向为逆时针,即为正方向,感应电流I′= ,C错误,D正确.
,C错误,D正确.
无
8.无
9. 由题意可知磁感应强度均匀减小,穿过闭合线圈的磁通量减小,根据楞次定律可以判断,圆环中产生顺时针方向的感应电流,圆环具有扩张的趋势,故A错误,B正确;圆环中产生的感应电动势为E= =
= S=|
S=| πr2k|,圆环的电阻为R=ρ
πr2k|,圆环的电阻为R=ρ =
=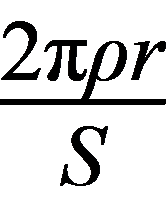 ,所以圆环中感应电流的大小为I=
,所以圆环中感应电流的大小为I= =|
=|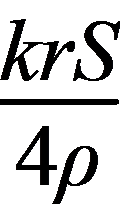 |,故C错误;图中a、b两点间的电势差Uab=I×
|,故C错误;图中a、b两点间的电势差Uab=I× R=|
R=| πkr2|,故D正确.
πkr2|,故D正确.
1.
(1)金属弦靠近螺线管时,线圈中磁场变强,根据楞次定律可得通过放大器的电流方向为向下.
(2)感应电动势的大小与磁通量的变化率有关,与线圈匝数有关,所以选项B、C正确;电吉他通过扩音器发出的声音频率与感应电流的频率相同,即与金属弦振动频率相同,A错误,D正确.
2.(1)由法拉第电磁感应定律得
E=n =n×
=n× ×(
×( )2
)2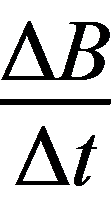 =10×
=10× ×(
×( )2×0.5 V=0.4 V.
)2×0.5 V=0.4 V.
(2)I= =0.4 A,P=I2r=0.16 W.
=0.4 A,P=I2r=0.16 W.
(3)分析线圈受力可知,当细线松弛时有:
F安=nBt0I =mg,I=
=mg,I=
Bt0= =2 T
=2 T
由图象知:Bt0=1+0.5t0(T),
解得t0=2 s.
3.(1)无论磁场方向是竖直向上还是竖直向下,当两金属细杆都以速度v朝相反方向滑动时,两金属细杆产生大小相同方向一致的感应电动势.
E1=E2=Bdv①
由闭合电路欧姆定律,回路中的电流
I= ②
②
因拉力与安培力平衡,作用于每根金属杆的拉力大小为F1=F2=BdI③
由①②③联立并代入数据,得F1=F2= =
= N=3.2×10-2 N.
N=3.2×10-2 N.
(2)设金属杆之间增加的距离为ΔL,则两金属杆共产生的热量Q=I2·2r· ,
,
代入数据得Q=1.28×10-2 J.
4.当ab杆沿导轨上滑达到最大速度v时,其受力如图所示:
由平衡条件可知:
F-FB=mgsin θ ①
又FB=BIL ②
 而I=
而I= ③
③
联立①②③式得:F- -mgsin θ=0 ④
-mgsin θ=0 ④
同理可得,ab杆沿导轨下滑达到最大速度时:mgsin θ- =0
=0
联立④⑤两式解得:F=2mgsin θ
v= .
.
第十二张
多选题
1.
根据题意,由动能定理对导体棒有:W1=Ek①,故A错误,C正确;根据能量守恒知W2-W1=Q ②,故B正确;对磁铁有:WF+WG-W2=0③,由①②③得WF+WG=Ek+Q,故D正确.
2.由E=Blv和I= 得I=
得I=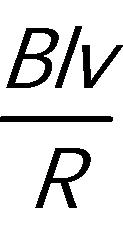 ,所以安培力F=BIl=
,所以安培力F=BIl= ,电阻上产生的热功率P=I2R=
,电阻上产生的热功率P=I2R= ,外力对ab杆做功的功率就等于回路产生的热功率.
,外力对ab杆做功的功率就等于回路产生的热功率.
两次拉出的速度之比v1∶v2=3∶1.电动势之比E1∶E2=3∶1,电流之比I1∶I2=3∶1,则电荷量之比q1∶q2=(I1t1)∶(I2t2)=1∶1.安培力之比F1∶F2=3∶1,则外力做功之比W1∶W2=3∶1,故C正确.
4.闭合S时,由于L的自感作用,A灯逐渐变亮,B灯立即变亮,稳定时两灯一样亮,故A错,B对;断开S时,由于L的自感作用,A、B两灯都不会立即熄灭,通过A灯的电流方向不变,但通过B灯的电流反向,故C错;又因通过A灯的电流不会比原来的大,故A灯不会闪亮一下再熄灭,故D错.
5.0~L过程中,ab边切割磁感线产生的感应电动势E1=BLv,a点电势高于b,则Uab= BLv;L~2L过程中感应电动势E2=2BLv,a点电势低于b,则Uab=-
BLv;L~2L过程中感应电动势E2=2BLv,a点电势低于b,则Uab=- BLv<0;2L~3L过程中,最左边切割磁感线产生的感应电动势E3=3BLv,a点电势高于b,则Uab=
BLv<0;2L~3L过程中,最左边切割磁感线产生的感应电动势E3=3BLv,a点电势高于b,则Uab= ×3BLv=
×3BLv=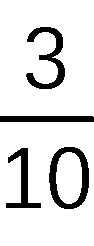 BLv,故D正确,A、B、C错误.
BLv,故D正确,A、B、C错误.
边长为L的正方形线框,从图示位置开始沿光滑斜面向下滑动,若进入磁场时所受安培力与重力沿斜面方向的分力平衡,则线框做匀速直线运动,感应电流为一恒定值;完全进入后磁通量不变,感应电流为零,线框做匀加速直线运动;从磁场中出来时,感应电流方向相反,所受安培力大于重力沿斜面方向的分力,线框做加速度减小的减速运动,感应电流减小,选项B正确.同理可知,C正确.
7.当外力F拉着金属杆匀速上升时,拉力要克服重力和安培力做功,拉力做的功等于克服安培力和重力做功之和,即等于电阻R上产生的热量和金属杆增加的重力势能之和,选项A错误,D正确.克服安培力做多少功,电阻R上就产生多少热量,选项B正确.电流做的功不等于重力势能的增加量,选项C错误.综上所述,本题的正确选项为B、D.
填空题1.
ΔΦ=Φ2-Φ1=BSsin 30°-0= Bπr2.
Bπr2.
又Δt= =
= =π/(6ω)
=π/(6ω)
所以 =
= =
= =3Bωr2.
=3Bωr2.
1.
(1)刚进入磁场时,a0=10 m/s2
方向竖直向上
由牛顿第二定律有BI0L-mg=ma0
若进入磁场时的速度为v0,有
I0= ,E0=BLv0
,E0=BLv0
得v0=
代入数值有:v0=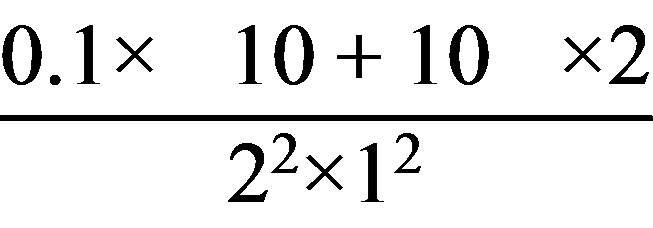 m/s=1 m/s
m/s=1 m/s
下落0.3 m时,通过a—h图象知a=0,表明金属杆受到的重力与安培力平衡有mg=BIL其中I= ,E=BLv,
,E=BLv,
可得下落0.3 m时杆的速度v=
代入数值有:
v= m/s=0.5 m/s.
m/s=0.5 m/s.
(2)从开始到下落0.3 m的过程中,由能量守恒定律有mgh=Q+ mv2
mv2
代入数值有Q=0.287 5 J
2.(1)设两根导线的总的张力的大小为T,右斜面对ab棒的支持力的大小为N1,作用在ab棒上的安培力的大小为F,左斜面对cd棒的支持力大小为N2.对于ab棒,由力的平衡条件得
2mgsin θ=μN1+T+F ①
N1=2mgcos θ ②
对于cd棒,同理有mgsin θ+μN2=T ③
N2=mgcos θ ④
联立①②③④式得
F=mg(sin θ-3μcos θ). ⑤
(2)由安培力公式得F=BIL ⑥
这里I是回路abdca中的感应电流.
ab棒上的感应电动势为E=BLv ⑦
式中,v是ab棒下滑速度的大小.
由欧姆定律得I= ⑧
⑧
联立⑤⑥⑦⑧式得v=(sin θ-3μcos θ) .
.
(1)棒在0~0.3 s内通过的电荷量q1= Δt1
Δt1
平均感应电流 =
=
回路中平均感应电动势 =
=
得q1=
同理,棒在0.3~0.4 s内通过的电荷量
q2=
由图象读出0.4 s时刻位移大小x2=0.9 m
又q1=2q2
解得x1=0.6 m.
(2)由图象知棒在0.3~0.4 s内做匀速直线运动,棒的速度大小v= m/s=3 m/s
m/s=3 m/s
对系统,根据能量守恒定律
Q=Mgx2-mgx2sin θ- (M+m)v2
(M+m)v2
代入数据解得Q=3.15 J
根据焦耳定律有 =
=
代入数据解得Q1=3 J.
化学
第一张
单选题
1.
燃烧热是反应热的一种,燃烧热特指101 kPa下,1 mol纯物质完全燃烧生成稳定的氧化物时放出的热量。燃烧反应都是放热反应,用文字描述燃烧热时通常不带正负号,但用ΔH表示燃烧热时,带负号,故选A。
2.A、依据化学反应方程式:N2(g)+3H2(g) 2NH3(g)+92kJ,反应是放热反应,依据能量守恒,反应物总能量大于生成物总能量,故A错误;B、已知:N2(g)+3H2(g)
2NH3(g)+92kJ,反应是放热反应,依据能量守恒,反应物总能量大于生成物总能量,故A错误;B、已知:N2(g)+3H2(g) 2NH3(g)+92kJ,反应是放热反应,依据能量守恒,反应物总能量大于生成物总能量,1 mol N2(g)和3 mol H2(g)的能量之和高于2 mol NH3 (g)的能量,故B正确;C、反应是可逆反应不能进行彻底,向密闭容器中通入1mol氮气和3mol氢气发生反应,放出的热量小于92.4 kJ,故C错误;D、已知:N2(g)+3H2(g)
2NH3(g)+92kJ,反应是放热反应,依据能量守恒,反应物总能量大于生成物总能量,1 mol N2(g)和3 mol H2(g)的能量之和高于2 mol NH3 (g)的能量,故B正确;C、反应是可逆反应不能进行彻底,向密闭容器中通入1mol氮气和3mol氢气发生反应,放出的热量小于92.4 kJ,故C错误;D、已知:N2(g)+3H2(g) 2NH3(g)+92 kJ,正反应是放热反应,则逆反应为吸热反应,即形成1 mol氮氮键和3 mol氢氢键所放出的能量比拆开6 mol氮氢键所吸收的能量少92 kJ,故D错误。故选B。
2NH3(g)+92 kJ,正反应是放热反应,则逆反应为吸热反应,即形成1 mol氮氮键和3 mol氢氢键所放出的能量比拆开6 mol氮氢键所吸收的能量少92 kJ,故D错误。故选B。
根据盖斯定律,(2)×2+(3)−(1)得2C(s)+2H2(g)+O2(g)  CH3COOH(l) ΔH=ΔH2×2+ΔH3−ΔH1=−488.3 kJ/ mol,故选A。
CH3COOH(l) ΔH=ΔH2×2+ΔH3−ΔH1=−488.3 kJ/ mol,故选A。
A.燃烧热是1 mol可燃物完全燃烧生成稳定氧化物反应放出的热量,1 mol碳不完全燃烧释放的能量是110.5 kJ,则碳的燃烧热大于 110.5 kJ/ mol,故A正确;B.C(石墨,s)  C(金刚石,s) ΔH=+1.9kJ· mol−1,说明石墨的能量比金刚石低,则石墨比金刚石稳定,故B错误;C.OH−(aq) + H+(aq)
C(金刚石,s) ΔH=+1.9kJ· mol−1,说明石墨的能量比金刚石低,则石墨比金刚石稳定,故B错误;C.OH−(aq) + H+(aq)  H2O(l) ΔH=−57.4 kJ· mol−1,即在稀溶液中1 mol NaOH与强酸完全反应生成1 mol水时,放出57.4 kJ热量,但醋酸是弱酸,其电离时需要吸热,则含20 g NaOH的稀溶液与过量稀醋酸完全反应,放出的热量应小于28.7 kJ,故C错误;D.固体硫燃烧时要先变为气态硫,过程吸热,气体与气体反应生成气体比固体和气体反应生成气体产生热量多,但反应热为负值,所以ΔH1<ΔH2;故D错误;故答案为A。
H2O(l) ΔH=−57.4 kJ· mol−1,即在稀溶液中1 mol NaOH与强酸完全反应生成1 mol水时,放出57.4 kJ热量,但醋酸是弱酸,其电离时需要吸热,则含20 g NaOH的稀溶液与过量稀醋酸完全反应,放出的热量应小于28.7 kJ,故C错误;D.固体硫燃烧时要先变为气态硫,过程吸热,气体与气体反应生成气体比固体和气体反应生成气体产生热量多,但反应热为负值,所以ΔH1<ΔH2;故D错误;故答案为A。
【错因分析】即在稀溶液中强酸与强酸完全反应生成1 mol水时,放出57.4kJ热量,但醋酸是弱酸,其电离时需要吸热,如忽略此点会错选C项。
5.本题主要考查燃烧热、中和热和反应热的概念。A中CO不是稳定氧化物,不能表示燃烧热,故A错;①的反应热应表示为−221 kJ/mol,故B错;醋酸电离吸热 ,因此与稀NaOH溶液反应生成1 mol水时放出的热量小于57.3 kJ,故D错。答案选C。
,因此与稀NaOH溶液反应生成1 mol水时放出的热量小于57.3 kJ,故D错。答案选C。
由于H—Br键的键长在H—Cl键和H—I键键长之间,所以其键能在H—Cl键和H—I键之间,A正确。表中H—F键的键能最大,所以H—F键最稳定,B正确。1 mol H2断裂1 mol H—H键吸收436 kJ能量,C正确。D项,ΔH=反应物的总键能-生成物的总 键能= (436+157-568×2) kJ·mol−1=−543 kJ·mol−1,D错误。
键能= (436+157-568×2) kJ·mol−1=−543 kJ·mol−1,D错误。
1.
(1)2N2H4(l)+N2O4(l)  3N2(g)+4H2O(g) ΔH2=−1048.5 kJ· mol−1 (2)400.5
3N2(g)+4H2O(g) ΔH2=−1048.5 kJ· mol−1 (2)400.5
【分析】(1)肼可作为火箭发动机的燃料,与氧化剂N2O4反应生成N2和水蒸气。①N2(g)+2O2(g)  N2O4(l) ΔH1=−19.5kJ· mol−1,②N2H4(l)+O2(g)
N2O4(l) ΔH1=−19.5kJ· mol−1,②N2H4(l)+O2(g)  N2(g)+2H2O(g) ΔH2=−534kJ· mol−1,根据盖斯定律,将方程式②×2−①得: 2N2H4(l)+N2O4(l)
N2(g)+2H2O(g) ΔH2=−534kJ· mol−1,根据盖斯定律,将方程式②×2−①得: 2N2H4(l)+N2O4(l)  3N2(g)+4H2O(g) ΔH=−1048.5kJ/ mol,故答案为:2N2H4(l)+N2O4(l)
3N2(g)+4H2O(g) ΔH=−1048.5kJ/ mol,故答案为:2N2H4(l)+N2O4(l)  3N2(g)+4H2O(g) ΔH=−1048.5kJ/ mol;
3N2(g)+4H2O(g) ΔH=−1048.5kJ/ mol;
(2) 设断裂1 molN−H键所需的能量为K kJ,根据N2H4(l)+O2(g)  N2(g)+2H2O(g) ΔH2=−534 kJ· mol−1,反应的焓变ΔH=反应物总键能−生成物总键能=(154+4K+500)−(942+4×462)=−534,解得K=400.5,故答案为:400.5。
N2(g)+2H2O(g) ΔH2=−534 kJ· mol−1,反应的焓变ΔH=反应物总键能−生成物总键能=(154+4K+500)−(942+4×462)=−534,解得K=400.5,故答案为:400.5。
【错因分析】不能根据化学键的键能进行吸热或放热的计算,将无法得到正确结果。
2.(1)双氧水是一种含有氧氧共价键和氧氢共价键的极性分子,电子式为: ;
;
已知0.4 mol液态肼和足量双氧水反应生成氮气和水蒸气时放出256.65 kJ的热量,1 mol液态肼反应放出的热量为: kJ=641.63kJ,则肼和双氧水反应的热化学方程式:N2H4(l)+2H2O2(l)
kJ=641.63kJ,则肼和双氧水反应的热化学方程式:N2H4(l)+2H2O2(l) N2(g)+4H2O(g) ΔH=−641.63 kJ/ mol;
N2(g)+4H2O(g) ΔH=−641.63 kJ/ mol;
(2)16g液态肼物质的量= =0.5 mol,由①N2H4(l)+2H2O2(l)
=0.5 mol,由①N2H4(l)+2H2O2(l) N2(g)+4H2O(g) ΔH=−641.63kJ/ mol;②H2O(l)
N2(g)+4H2O(g) ΔH=−641.63kJ/ mol;②H2O(l) H2O(g) ΔH=+44 kJ/ mol,结合盖斯定律,将①−4×②得,N2H4(l)+2H2O2(l)
H2O(g) ΔH=+44 kJ/ mol,结合盖斯定律,将①−4×②得,N2H4(l)+2H2O2(l) N2(g)+4H2O(l) ΔH=−817.63 kJ/ mol,所以0.5 mol液态肼与足量双氧水反应生成氮气和液态水时,放出的热量=0.5 mol×817.63 kJ/ mol=408.8 kJ;
N2(g)+4H2O(l) ΔH=−817.63 kJ/ mol,所以0.5 mol液态肼与足量双氧水反应生成氮气和液态水时,放出的热量=0.5 mol×817.63 kJ/ mol=408.8 kJ;
(3))①N2(g)+2O2(g) 2NO2(g) ΔH=+67.7 kJ· mol−1;②N2H4(g)+O2(g)
2NO2(g) ΔH=+67.7 kJ· mol−1;②N2H4(g)+O2(g) N2(g)+2H2O (g) ΔH=−534 kJ· mol−1,根据盖斯定律,将②×2−①得2N2H4(g)+2NO2(g)
N2(g)+2H2O (g) ΔH=−534 kJ· mol−1,根据盖斯定律,将②×2−①得2N2H4(g)+2NO2(g) 3N2(g)+4H2O(g) ΔH=2×(−534 kJ· mol−1)−(+67.7kJ· mol−1)=−1135.7 kJ· mol−1,肼与NO2完全反应生成氮气和气态水的热化学方程式为2N2H4(g)+2NO2(g)
3N2(g)+4H2O(g) ΔH=2×(−534 kJ· mol−1)−(+67.7kJ· mol−1)=−1135.7 kJ· mol−1,肼与NO2完全反应生成氮气和气态水的热化学方程式为2N2H4(g)+2NO2(g) 3N2(g)+4H2O(g) ΔH=−1135.7 kJ· mol−1。
3N2(g)+4H2O(g) ΔH=−1135.7 kJ· mol−1。
根据盖斯定律①− ②,可得反应③的ΔH=89.3kJ/mol;
第二张
单选题
1.
ΔH<0、ΔS>0,则ΔH-TΔS<0,任何温度下反应都能自发进行,A正确,B正确;用焓变和熵变判断反应的自发性,都有例外,故都不能单独作为反应自发性的判据,而应用复合判据,C错误;使用催化剂能改变反应的活化能,因此能改变化学反应进行的速率。D正确。
2.根据v=Δc/Δt计算。根据4A(g)+B(g)=2C(g),生成C为0.2 mol,反应的A为0.4 mol,则用反应物A浓度的减少来表示该反应的速率应为υ(A)= =0.05 mol/(L·s),故选C。
=0.05 mol/(L·s),故选C。
【错因分析】注意要求的是用反应物A的速率来表示,若算成B或C的反应速率,会导致错误。
3.因为SO3的浓度增加了0.8 mol·L-1,所以O2的浓度减少了0.4 mol·L-1,因为在这段时间内用O2表示的反应速率为0.04 mol·L-1·s-1,所以反应所需时间为10 s。
4.在0~50 min之间,pH=2和pH=7时反应物R都能完全反应,降解率都是100%,故A正确;由斜率可知pH越小降解速率越大,即溶液的酸性越强,R的降解速率越大,故B错误;浓度越大化学反应速率越大,所以起始浓度越小降解速率越小,故C错误;20~25 min之间,pH=10时R的平均降解速率为,故D错误。
5.根据v=Δc/Δt计算。根据4A(g)+B(g)=2C(g),生成C为0.2 mol,反应的A为0.4 mol,则用反应物A浓度的减少来表示该反应的速率应为υ(A)= =0.05 mol/(L·s),故选C。
=0.05 mol/(L·s),故选C。
【错因分析】注意要求的是用反应物A的速率来表示,若算成B或C的反应速率,会导致错误。
6.A.2s~4s时间内氨气的浓度变化为:(1.4−1.0) mol/L=0.4 mol/L,平均反应速率为: =0.2 mol/(L·s),故A正确;B.前4s时间内氨气的浓度变化为:(1.4−0.2) mol/L=1.2 mol/L,平均反应速率为:
=0.2 mol/(L·s),故A正确;B.前4s时间内氨气的浓度变化为:(1.4−0.2) mol/L=1.2 mol/L,平均反应速率为: =0.3 mol/(L·s),故B正确;C.前2s时间内氨气的浓度变化为:(1.0−0.2) mol/L=0.8 mol/L,氨气的平均反应速率为:
=0.3 mol/(L·s),故B正确;C.前2s时间内氨气的浓度变化为:(1.0−0.2) mol/L=0.8 mol/L,氨气的平均反应速率为: =0.4 mol/(L·s),故C正确;D.2s内氨气的平均速率为0.4 mol·(L·s)−1,不是即时速率,故D错误;故答案为D。
=0.4 mol/(L·s),故C正确;D.2s内氨气的平均速率为0.4 mol·(L·s)−1,不是即时速率,故D错误;故答案为D。
在分析有关图像时应该注意:v−t图像要分清正逆反应,分清各因素(浓度、温度、压强、催化剂)对反应速率和平衡移动的影响;在转化率−时间图像或物质的百分含量−时间图像中,先出现拐点的曲线先达到平衡,代表温度高或压强大或使用合适的催化剂等。A项、增大氧气的浓度,平衡破坏的瞬间逆反应速率应不变,图中条件变化应为增大压强,故A错误;B项、图Ⅱ中正、逆反应速率同等程度的增大,化学平衡不移动,应为催化剂对反应速率的影响,故B正确;C项、催化剂能同等程度改变正逆反应速率,但平衡不移动,图中条件变化应为压强对平衡的影响,故C错误;D项、图像Ⅲ中乙首先到达平衡状态,则乙的温度高于甲中的温度,故D错误。故选B。
【错因分析】本题考查影响化学平衡的因素及图象,注意压强、浓度、催化剂对反应速率及平衡的影响,把握图中速率的关系及点、线、面的意义是解答关键。如果不明白外界因素对化学反应速率的影响,不能抓住影响反应速率的实质(是浓度变化引起的,还是加入催化剂引起的),将会错解。
8.A项,根据图示 CH4与CO2在催化剂存在时生成CH3COOH,总反应为CH4+CO2
CH4与CO2在催化剂存在时生成CH3COOH,总反应为CH4+CO2 CH3COOH,只有CH3COOH一种生成物,原子利用率为100%,A项正确;B项,CH4选择性活化变为①过程中,有1个C-H键发生断裂,B项正确;C项,根据图示,①的总能量高于②的总能量,①→②放出能量,对比①和②,①→②形成C-C键,C项正确;D项,催化剂只影响化学反应速率,不影响化学平衡,不能提高反应物的平衡转化率,D项错误;答案选D。
CH3COOH,只有CH3COOH一种生成物,原子利用率为100%,A项正确;B项,CH4选择性活化变为①过程中,有1个C-H键发生断裂,B项正确;C项,根据图示,①的总能量高于②的总能量,①→②放出能量,对比①和②,①→②形成C-C键,C项正确;D项,催化剂只影响化学反应速率,不影响化学平衡,不能提高反应物的平衡转化率,D项错误;答案选D。
1.
(1)根据题意:A、C的化学计量数之比为0.09∶0.06=3∶2,再根据改变压强,平衡不移动可知反应为等体反应,所以方程式为3A(g)  2C(g)+B(g)。故c(B)=(0.05-0.03) mol·L-1=0.02 mol·L-1。
2C(g)+B(g)。故c(B)=(0.05-0.03) mol·L-1=0.02 mol·L-1。
(2)升温,v(正)>v(逆),反应为吸热反应,故热化学方程式为3A(g) B(g)+2C(g) ΔH= +100akJ·mol−1。
B(g)+2C(g) ΔH= +100akJ·mol−1。
(3)t3时,改变条件,v(正)=v(逆)、增大,又因反应为等体反应,故条件为增大压强或使用催化剂。
(4)恒温恒压下通入惰性气体,相当于减压,等体反应平衡不移动,v(正)=v(逆)。
2.(1)H2还原氧化钴的方程式为:H2(g)+CoO(s) Co(s)+H2O(g);CO还原氧化钴的方程式为:CO(g)+CoO(s)
Co(s)+H2O(g);CO还原氧化钴的方程式为:CO(g)+CoO(s) Co(s)+CO2(g),平衡时H2还原体系中H2的物质的量分数(
Co(s)+CO2(g),平衡时H2还原体系中H2的物质的量分数(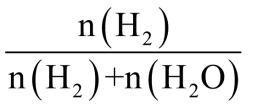 )高于CO还原体系中CO的物质的量分数(
)高于CO还原体系中CO的物质的量分数( ),故还原CoO(s)为Co(s)的倾向是CO大于H2;
),故还原CoO(s)为Co(s)的倾向是CO大于H2;
(2)721 ℃时,在密闭容器中将等物质的量的CO(g)和H2O(g)混合,可设其物质的量为1mol,则
CO(g)+H2O(g) CO2(g)+H2(g)
CO2(g)+H2(g)
起始(mol) 1 1 0 0
转化(mol) x x x x
平衡(mol) 1-x 1-x x x
则平衡时体系中H2的物质的量分数= ,因该反应为可逆反应,故x<1,可假设二者的还原倾向相等,则x=0.5,由(1)可知CO的还原倾向大于H2,所以CO更易转化为H2,故x>0.5,由此可判断最终平衡时体系中H2的物质的量分数介于0.25~0.50,故答案为C;
,因该反应为可逆反应,故x<1,可假设二者的还原倾向相等,则x=0.5,由(1)可知CO的还原倾向大于H2,所以CO更易转化为H2,故x>0.5,由此可判断最终平衡时体系中H2的物质的量分数介于0.25~0.50,故答案为C;
(3)根据水煤气变换[CO(g)+H2O(g)=CO2(g)+H2(g)]并结合水煤气变换的反应历程相对能量可知,CO(g)+H2O(g)的能量(-0.32eV)高于CO2(g)+H2(g)的能量(-0.83eV),故水煤气变换的ΔH小于0;活化能即反应物状态达到活化状态所需能量,根据变换历程的相对能量可知,最大差值为:

其最大能垒(活化能)E正=1.86-(-0.16)eV=2.02eV;该步骤的反应物为COOH +H
+H +H2O
+H2O =COOH
=COOH +2H
+2H +OH
+OH ;因反应前后COOH
;因反应前后COOH 和1个H
和1个H 未发生改变,也可以表述成H2O
未发生改变,也可以表述成H2O =H
=H +OH
+OH ;
;
(4)由图可知,30~90 min内a曲线对应物质的分压变化量Δp=(4.08-3.80)kPa=0.28 kPa,故曲线a的反应在30~90 min内的平均速率 (a)=
(a)= =0.0047 kPa·min−1;由(2)中分析得出H2的物质的量分数介于0.25~0.5,CO的物质的量分数介于0~0.25,即H2的分压始终高于CO的分压,据此可将图分成两部分:
=0.0047 kPa·min−1;由(2)中分析得出H2的物质的量分数介于0.25~0.5,CO的物质的量分数介于0~0.25,即H2的分压始终高于CO的分压,据此可将图分成两部分:

由此可知,a、b表示的是H2的分压,c、d表示的是CO的分压,该反应为放热反应,故升高温度,平衡逆向移动,CO分压增加,H2分压降低,故467 ℃时PH2和PCO随时间变化关系的曲线分别是b、c;489 ℃时PH2和PCO随时间变化关系的曲线分别是a、d。
第三张
单选题
1.
ΔH<0、ΔS>0,则ΔH-TΔS<0,任何温度下反应都能自发进行,A不正确,B正确;用焓变和熵变判断反应的自发性,都有例外,故都不能单独作为反应自发性的判据,而应用复合判据,C错误;使用催化剂能改变反应的活化能,因此能改变化学反应进行的速率,但不能改变转化率,D正确。
2.一定条件下,乙烷发生分解反应:C2H6 C2H4+H2,一段时间后,各物质的浓度保持不变说明反应达到平衡状态,A.浓度保持不变说明反应达到平衡状态,故A正确;B.化学平衡是动态平衡,C2H6仍在不断分解,其浓度保持不变,故B错误;C.达到平衡状态正逆反应速率相同,所以C2H6的分解速率等于生成速率,故C错误;D.化学平衡是动态平衡,C2H6仍在不断分解,其浓度保持不变,故D错误。故选A。
C2H4+H2,一段时间后,各物质的浓度保持不变说明反应达到平衡状态,A.浓度保持不变说明反应达到平衡状态,故A正确;B.化学平衡是动态平衡,C2H6仍在不断分解,其浓度保持不变,故B错误;C.达到平衡状态正逆反应速率相同,所以C2H6的分解速率等于生成速率,故C错误;D.化学平衡是动态平衡,C2H6仍在不断分解,其浓度保持不变,故D错误。故选A。
平衡常数K值越大,反应向正反应进行的程度越大,X的转化率越大,A项正确。达平衡时2v正(X)=v逆(Z),B项错误。达平衡后降低温度,正、逆反应速率均减小,又因平衡向正反应方向移动,所以正反应速率减小的倍数小于逆反应速率减小的倍数,C项错误。增大压强平衡不移动,升高温度平衡逆向移动,D项错误。
4.A项,反应速率越快,达到化学平衡所需的时间越短,所以b代表20 ℃下CH3COCH3的Y t曲线。B项,由题图可知,20 min时a曲线对应点的斜率小于b曲线,所以CH3COCH3的<1。C项,由题图可知,20 ℃时CH3COCH3的平衡转化率一定小于0 ℃时的平衡转化率。D项,当Y=0.113时,a曲线与b曲线相交,故产物量相同。
t曲线。B项,由题图可知,20 min时a曲线对应点的斜率小于b曲线,所以CH3COCH3的<1。C项,由题图可知,20 ℃时CH3COCH3的平衡转化率一定小于0 ℃时的平衡转化率。D项,当Y=0.113时,a曲线与b曲线相交,故产物量相同。
本题考查了化学平衡状态的判断,注意把握化学平衡状态判断的角度,特别是正逆反应速率的关系,为易错点。①如果该反应是一个反应前后气体体积不变的可逆反应,则体系的压强始终不变,所以不能根据压强判断反应是否达到平衡状态,故错误;②体系的温度不再改变,正逆反应速率相等,所以能据此判断该反应达到平衡状态,故正确;③各组分的物质的量浓度不再改变,该反应达到平衡状态,故正确;④当该反应达到平衡状态,各组分的质量分数不再改变,故正确;⑤当反应速率vA∶vB∶vC∶vD=m∶n∶p∶q,不能据此判断该反应是否达到平衡状态,故错误;⑥单位时间内m mol A断键反应等效于p mol C形成,同时p mol C也断键反应,故正确;故选B。
【错因分析】反应达到平衡状态时,正、逆反应速率相等,各物质的浓度、百分含量不变,由此衍生出来的各种量不变。需要注意的是,选择判断的物理量,随着反应的进行发生变化,当该物理量由变量变为定值时,说明可逆反应达到平衡状态。若不清楚有可能存在m+n=p+q,体系压强始终不变,则易错选①,若不清楚反应速率之比始终存在v(A)∶v(B)∶v(C)∶v(D)=m∶n∶p∶q,与是否达到平衡状态无关,易错选⑤。
6. 3A(g)+2B(g)  4C(?)+2D(?)
4C(?)+2D(?)
开始(mol/L):2 1 0 0
转化(mol/L):0.6 0.4 0.8 0.4
平衡(mol/L):1.4 0.6 0.8 0.4
设平衡时气体总的物质的量浓度为x mol/L,根据压强之比等于物质的量之比可得: , 又因为
, 又因为 ,故
,故 ,可得x=2.4,从而可知C为固体或液体,D为气体。故化学平衡常数的表达式为:K=
,可得x=2.4,从而可知C为固体或液体,D为气体。故化学平衡常数的表达式为:K= ,①错误;B的转化率为40%,②错误;该反应是一个反应后气体分子数减小的反应,增大压强,平衡向右移动,平衡常数只与温度有关,温度不变平衡常数不变,③正确;由于C为固体或液体,增加C的量,平衡不发生移动,A、B的转化率不变,④正确。
,①错误;B的转化率为40%,②错误;该反应是一个反应后气体分子数减小的反应,增大压强,平衡向右移动,平衡常数只与温度有关,温度不变平衡常数不变,③正确;由于C为固体或液体,增加C的量,平衡不发生移动,A、B的转化率不变,④正确。
1.
(1)+113
(2)①0.04 mol/(L·min) 40% ②A
(3)①> ②升高温度 ③0.0125MPa(单位可不带) 恒压条件下,增大氩气的比例,相当于减压,从而使平衡正向移动,提高了丙烷的平衡转化率
【分析】(1)反应热ΔH=反应物总键能−生成物总键能=(2×332+8×414)−(6×414+332+611+436) kJ/ mol =+113 kJ/ mol,故答案为:+113;
(2)一定温度下,向2L的密闭容器中充入2 molC3H8发生脱氧反应,经过10min达到平衡状态,测得平衡时气体压强是开始的1.4倍,则反应后气体总物质的量= ×2 mol =2.8 mol。
×2 mol =2.8 mol。
①设生成的丙烯物质的量为x mol,
可逆反应C3H8(g)  C3H6(g)+H2(g)
C3H6(g)+H2(g)
开始( mol) 2 0 0
反应( mol) x x x
平衡( mol) 2−x x x
反应后气体总物质的量=(2−x+x+x) mol=2.8 mol,x=0.8,0~10min内氢气的生成速率v(H2)= =
= =0.04 mol/(L·min);C3H8的平衡转化率=
=0.04 mol/(L·min);C3H8的平衡转化率= ×100%=
×100%= ×100%=40%,故答案为:0.04 mol/(L·min);40%;
×100%=40%,故答案为:0.04 mol/(L·min);40%;
②A. C3H8分解速率与 C3H6消耗速率相等,C3H6也等于的生成速率,正逆反应速率相等,反应达到平衡状态,故A正确;B. 根据方程式C3H6与H2的物质的量之比始终保持不变,不能说明反应达到平衡状态,故B错误;C.反应前后气体总质量不变、容器体积不变,则气体密度始终保持不变,不能据此判断平衡状态,故C错误;答案选A;
(3)①根据图像,随温度升高,丙烯的物质的量分数增加,丙烷的物质的量分数减少,说明升温平衡正向进行,正反应为吸热反应,反应的ΔH>0;C3H8(g)⇌C3H6(g)+H2(g),温度一定时,压强越大,平衡逆向进行,p2压强下丙烯物质的量分数大于p1状态,说明p1>p2,平衡正向进行,故答案为:>;
②增大化学反应速率的方法有:增大浓度、升高温度、加入催化剂、增大压强等,增大转化率的方法有:减小压强、升高温度、减小生成物浓度等,所以要增大反应速率和增大转化率需要改变的条件是升高温度,故答案为:升高温度;
③设丙烷物质的量为1 mol,消耗物质的量为y mol,根据图像可知,丙烷在Q点物质的量分数为50%,
C3H8(g)  C3H6(g)+H2(g)
C3H6(g)+H2(g)
起始量( mol) 1 0 0
变化量( mol) y y y
平衡量( mol) 1−y y y
 =50%,y=
=50%,y= ,总物质的量=1+y=
,总物质的量=1+y= mol,平衡常数Kp=
mol,平衡常数Kp= =0.0125MPa,故答案为:0.0125MPa;
=0.0125MPa,故答案为:0.0125MPa;
④该反应为气体分子数增加的反应,随着氩气比例的增加,降低了反应体系各气体的分压,相当于减压,减小压强,平衡向气体体积增大的方向移动,从而提高丙烷脱氢转化率,故答案为:恒压条件下,增大氩气的比例,相当于减压,从而使平衡正向移动,提高了丙烷的平衡转化率。
2.(1)根据反应方程式知,HCl平衡转化率越大,平衡常数K越大,结合图像知升高温度平衡转化率降低,说明升高温度平衡向逆反应方向进行,则K(300℃)>K(400℃);
由图像知,400℃时,HCl平衡转化率为84%,用三段式法对数据进行处理得:

起始(浓度) c0c00 0
变化(浓度) 0.84c0 0.21c0 0.42c00.42c0
平衡(浓度)(1-0.84)c0 (1-0.21)c00.42c00.42c0
则K= ;根据题干信息知,进料浓度比过低,氧气大量剩余,导致分离产物氯气和氧气的能耗较高;进料浓度比过高,HCl不能充分反应,导致HCl转化率较低;
;根据题干信息知,进料浓度比过低,氧气大量剩余,导致分离产物氯气和氧气的能耗较高;进料浓度比过高,HCl不能充分反应,导致HCl转化率较低;
(2)根据盖斯定律知,(反应I+反应II+反应III)×2得 ∆H=(∆H1+∆H2+∆H3)×2=-116kJ·mol-1;
∆H=(∆H1+∆H2+∆H3)×2=-116kJ·mol-1;
(3)若想提高HCl的转化率,应该促使平衡正向移动,该反应为气体体积减小的反应,根据勒夏特列原理,可以增大压强,使平衡正向移动;也可以及时除去产物,减小产物浓度,使平衡正向移动;
第四张
单选题
1.
能发生银镜反应,说明有机物结构中含有醛基;已学过的能发生水解反应的有机物有卤代烃、酯及低聚糖或多糖等。甲酸甲酯中有 和
和 ;蔗糖能发生水解反应,但无
;蔗糖能发生水解反应,但无 ;葡萄糖能发生银镜反应,但不能水解;麦芽糖是还原性糖,能发生银镜反应,同时也能发生水解反应。
;葡萄糖能发生银镜反应,但不能水解;麦芽糖是还原性糖,能发生银镜反应,同时也能发生水解反应。
油脂在碱溶液的作用下发生的水解叫皂化反应,生成的是高级脂肪酸钠、甘油和水形成的混合液,加食盐细粒,可发生盐析,上层是高级脂肪酸钠,下层是甘油和食盐的混合溶液,可用过滤的方法分离提纯。
3.蚕丝、羊毛的主要成分是蛋白质,棉花的主要成分是纤维素;蛋白质溶液是胶体,能产生丁达尔效应;CuSO4是重金属盐,其溶液能使蛋白质发生变性;蛋白质在紫外线照射下会发生变性而失去生理活性。
4. B5.
碘用来检验淀粉,如变蓝意味着有淀粉存在,说明淀粉部分水解或没有水解。淀粉在稀硫酸存在下水解为葡萄糖,葡萄糖能使银氨溶液析出银。在本实验中如果有银析出,说明淀粉发生了水解。在进行银镜反应前要先中和催化剂——稀硫酸。
6. B7.
将蛋白质片段按 中C—N键断裂的方式切断,断开后
中C—N键断裂的方式切断,断开后 加—OH、—NH—加H,分别组装成各种氨基酸,再根据各氨基酸的结构,找出水解不可能产生的氨基酸。
加—OH、—NH—加H,分别组装成各种氨基酸,再根据各氨基酸的结构,找出水解不可能产生的氨基酸。
淀粉在淀粉酶作用下经足够长时间后,完全水解为葡萄糖,渗透到半透膜袋外的水中,而淀粉酶属于蛋白质,为高分子化合物,留在袋内,遇浓硝酸变黄色。
9.有银镜反应发生说明必有醛基,排除C;加入Zn粒无变化,说明分子中无—COOH,A错;加入Cu(OH)2悬溶液无变化,因为并未加热煮沸不能说明无醛基,但可以说明无—COOH,只有D符合题意。
10.葡萄糖分子中含有醛基,醛基有还原性,易把新制的氢氧化铜还原成氧化亚铜沉淀,A错;B对;棉花和麻的主要成分是纤维素而非蛋白质,C错;乙酸与羟基乙醛互为同分异构体,分子式均是C2H4O2,而甲酸乙酯的分子式是C3H6O2,不是它们的同分异构体,D错。
11. B12.
. 石油的分馏是物理变化,而煤的干馏属于化学变化,A项错误;C项淀粉、纤维素的聚合度(n)不同,不正确;蛋白质水解产物为氨基酸,含碳、氢、氧、氮等元素,D项不正确。
13. D14. C
15. B
16.
乙烯等短链不饱和烃主要是石油裂解过程中得到的产品;食盐中加的碘为碘酸钾而不是单质碘,不能用淀粉来检验食盐是否为加碘盐;油脂在碱性条件下的水解反应又叫皂化反应,可以用来制造肥皂;蛋白质的变性属于不可逆变化,变性后加水不再溶解.
17.油脂的水解是取代反应,A项正确;B、C、D中的反应均为氧化反应.
18.主要是与葡萄糖、淀粉、油脂、蛋白质等物质的性质有关的题目,难度不大。通过本题的分析解答,引导自己注重基本知识的复习与掌握,提高对基本知识应用的熟练程度。对葡萄糖、淀粉、油脂、蛋白质的结构和性质不清楚而导致误选。植物油是一种不饱和油脂,能和Br2发生加成反应,所以A不正确。淀粉是一种多糖,它水解的最终产物是葡萄糖,人摄入淀粉后通过水解成为葡萄糖进而提供能量,所以B正确。葡萄糖中含有醛基,能被氧化成葡萄糖酸,不能发生水解反应,C不正确。蛋白质溶液遇CuSO4等重金属盐溶液会发生变性,该过程不可逆,就是说产生的沉淀不能重新溶于水,D不正确。
19.只有准确把握住油脂属于酯类化合物,含官能团—COOR,另某些油脂的烃基中含不饱和键,有关油脂的问题可迎刃而解。本题要求选出“与其含有的不饱和双键有关”的性质,这是解题的关键,也是容易导致出错的地方。A、B、D三项是油脂的共性,与结构中是否含有双键无关。C中的“氢化”就是与H2的加成反应,是不饱和双键的特性。
20. D解答题
1.
淀粉水解产物为葡萄糖(A),其结构简式为CH2OH(CHOH)4CHO。由题给信息可知其中的—CHO 先被氧化,然后再是—CH2OH被氧化。看官能团变化前后原子数目的多少,若是—CHO被氧化,则相当于增加了一个氧原子,其他原子没变,则B(C6H12O7)是—CHO 被氧化的产物。分析C(C6H10O8),则多了两个氧原子,少了两个氢原子,则是—CHO与—CH2OH都被氧化成了—COOH。再分析D(C6H14O6)与原物质A(C6H12O6)相比较,多了两个氢原子,可认为是醛基被还原了(与H2加成)。
2.(1)B、C为能发生银镜反应的物质,其结构中一定含有—CHO,又因C能发生水解反应,故B、C应分别是葡萄糖与HCOOC2H5。(2)遇碘水显蓝色是淀粉。(3)HCOOC2H5、蔗糖、淀粉水解的产物均能发生银镜反应。
第五张
单选题
1. C
2. B
3. D
4. C
5. B
6. C
7. C
8. B
9. D
10. C
解答题
1.
11.(1)加成反应 Cu或Ag,加热
(2) 
(3)c (4)4
2.(1)醚键、羰基
(2)消去反应
(3) 
(4)CH(CHO)3
(5) 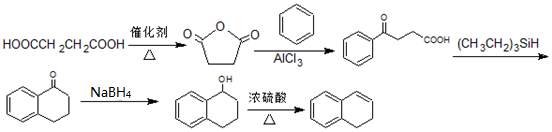
(1)醚键、羰基
(2)消去反应
(3) 
(4)CH(CHO)3
(5) 
第六张
单选题
1. C
2. A
3. A
4. B
5. B
6. D
7. A
8. C
9. B
10. B
11. B
解答题
1.
(1) 4 CH3COCH2CH2CH3 CH3COCH(CH3)2
CH3CH2COCH2CH3
(2) ①cd ② 4 ③ 7
2.⑴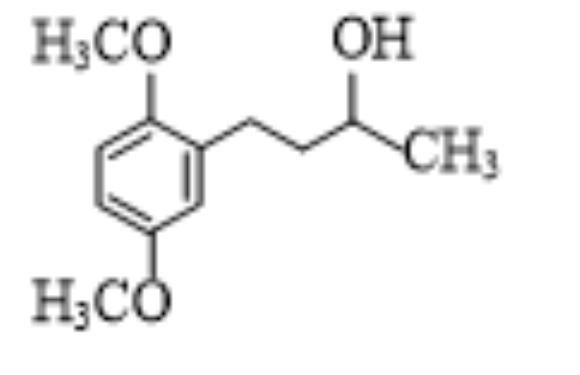
⑵
⑶sp3、sp
⑷1
⑸
第七张
单选题
1.
A、苯环能发生取代反应,羟基能发生取代反应,所以苯酚、环己醇都能发生取代反应,故A正确;
B、根据醇羟基与酚羟基都能与金属钠反应放出氢气,所以苯酚、环己醇都能与金属钠反应放出氢气,故B正确;
C、根据苯酚的酸性比碳酸弱,环己醇显中性,故C错误;
D、根据酚遇FeCl3溶液作用显紫色,而醇无此性质,所以苯酚与FeCl3溶液作用显紫色,环己醇加入FeCl3溶液中无明显现象,故D正确。
2.根据乙醇不会和NaOH溶液反应,加入NaOH溶液后,苯酚的乙醇溶液中,乙醇不会发生任何变化,但苯酚全部变成苯酚钠.这样原来的溶液就变成了苯酚钠、NaOH溶液(加入NaOH溶液是过量的)中混有乙醇.乙醇的沸点是78℃,水的沸点是100℃.这样加热到78℃,达到乙醇的沸点,乙醇被全部蒸馏掉,而剩下的苯酚钠、NaOH溶液不变.最后通入过量的二氧化碳气体,由于碳酸酸性强于苯酚酸性,所以加入二氧化碳后,NaOH先全部转化为NaHCO3(加入过量二氧化碳),然后苯酚钠全部转化为苯酚.苯酚不溶水,与生成的NaHCO3溶液分层,静置后分液可以得到苯酚,
故选D。
3.A、苯酚的浑浊液加热后变澄清,说明温度升高苯酚溶解度增大,无法说明苯酚的酸性,故A错误;
B、苯酚的水溶液中加NaOH溶液,生成苯酚钠,溶液变澄清,说明苯酚溶液呈酸性,故B正确;
C、苯酚与氯化铁溶液发生显色反应,无法说明苯酚的酸性,故C错误;
D、苯酚溶液中滴加紫色石蕊指示剂不变色,无法说明苯酚的酸性,故D错误。
4.A.氢氧化钠具有腐蚀性,会腐蚀皮肤,故A错误;
B.苯酚不溶于水,但易溶在酒精中,可以用酒精洗去,故B正确;
C.温度过高,会烫伤皮肤,故C错误;
D.苯酚不溶于水,难易除去沾有的苯酚,故D错误。
5.A.跟氢氧化钠溶反应生成苯酚钠,说明苯酚具有酸性,不能证明苯酚的酸性极弱,故A错误;
B.苯酚在空气中容易被氧化为粉红色,说明苯酚具有还原性,不能证明苯酚的酸性极弱,故B错误;
C.碳酸是弱酸,二氧化碳通入苯酚溶液能游离出苯酚,说明苯酚酸性比碳酸弱,故能证明苯酚的酸性极弱,故C正确;
D.常温下苯酚在水中溶解度不大,说明苯酚与水的极性不相似,不能证明苯酚的酸性极弱,故D错误。
6.A、由于苯酚水溶液显弱酸性,俗称石炭酸,故A正确;
B、由于苯酚有腐蚀性,苯酚若不慎沾在皮肤上,应立即用酒精擦洗,故B正确;
C、由于苯酚在水中的溶解度随温度的升高而增大,超过65℃可以与水以任意比互溶,故C正确;
D、由于苯酚酸性小于碳酸酸性,在碳酸氢钠溶液中滴入苯酚的水溶液,不会生成二氧化碳气体,故D错误。
7.由于羟基是很强的邻、对位定位基,酚中p﹣π共轭使苯环上的电子云密度增大,所以苯酚很容易发生亲电取代反应,且生成在酚羟基的邻、对位取代为主的产物,即羟基影响了苯环,使苯环上的氢原子变活泼,而导致苯酚比苯易发生取代反应,故选C。
8.A、由于苯必须与液溴反应,苯酚和浓溴水就可以发生反应,故A错误;
B、由于苯酚和浓溴水反应,不需要催化剂,故B正确;
C、由于苯与液溴生成一溴苯,苯酚与溴水生成三溴苯酚,故C错误;
D、由于苯和苯酚分别与溴反应都不需要加热,故D错误。
9.A.苯酚与浓溴水反应发生取代反应生成2,4,6﹣三溴苯酚,与苯酚酸性无关,故A错误;
B.苯酚的水溶液中加NaOH溶液,生成苯酚钠,只能说明苯酚溶液呈酸性,故B错误;
C.苯酚的浑浊液加热后变澄清,说明温度升高苯酚溶解度增大,但是不能说明苯酚的酸性强弱,故D错误;
D.碳酸是弱酸,与苯酚钠溶液反应生成苯酚,说明苯酚酸性比碳酸弱,故D正确。
10.甲苯中苯环对—CH3的影响,使—CH3可被KMnO4(H+)氧化为—COOH,从而使KMnO4溶液褪色;乙烯能与溴发生加成反应,是因为含碳碳双键;苯环对羟基产生影响,使羟基中氢原子更易电离,从而苯酚表现出弱酸性;苯酚中,羟基对苯环产生影响,使苯酚分子中羟基碳邻、对位碳上的氢原子变得活泼,更易被取代;A、C、D项符合题意,B项不合题意。
11.甲苯中苯环对—CH3的影响,使—CH3可被KMnO4(H+)氧化为—COOH,从而使KMnO4溶液褪色;乙烯能与溴发生加成反应,是因为含碳碳双键;苯环对羟基产生影响,使羟基中氢原子更易电离,从而苯酚表现出弱酸性;苯酚中,羟基对苯环产生影响,使苯酚分子中羟基碳邻、对位碳上的氢原子变得活泼,更易被取代;A、C、D项符合题意,B项不合题意。
12.A中,1 mol该物质每个苯环上可消耗2 mol Br2,共消耗4 mol Br2;B中,酚的酸性没有碳酸的强,不能与碳酸氢钠溶液反应生成CO2;C中,中间一个碳原子上连的四个碳构成空间四面体,不可能都在同一平面;D中,加成后不含双键,但有两个环,氢原子数为32-4=28。
13.A、苯酚可以和氢气发生加成反应生成环己烷,体现了苯酚中化学键的性质,故A错误;
B、苯酚能和NaOH溶液反应,说明苯酚具有弱酸性,能和碱反应生成盐和水,故B错误;
C、有机物大多是容易燃烧的,苯酚燃烧产生带浓烟的火焰体现了有机物的通性,故C错误;
D、苯酚和浓溴水反应生成三溴苯酚,体现了酚羟基的邻对位氢原子活泼,能说明侧链羟基对苯环性质有影响,故D正确。
14.A、苯酚在水中的溶解度较小,故A错误;
B、稀盐酸不能和酸性物质发生反应,不能消除苯酚的污染,故B错误;
C、苯酚虽然在酒精中的溶解度较大,但是苯酚与酒精在一起不能消除苯酚的污染,故C错误;
D、苯酚是显酸性的物质,苯酚能与强碱反应,所以处理苯酚的最佳方法是用石灰中和,故D正确。
15.由苏丹红的分子结构知该分子中含一个苯环和一个萘环,属于芳香族化合物,A项正确;苏丹红在萘环上有—OH,是酚类有机物,B项正确;苏丹红分子结构中苯环上有2个甲基侧链,故苏丹红能被酸性KMnO4溶液氧化,C项正确;苯环上的氢原子也可与Br2发生取代反应,D项错误。
16.A.溴易溶于苯,用溴水除杂,苯酚和溴水反应生成三溴苯酚,三溴苯酚是有机物,溶于苯中,同时会引入新的杂质,则除去苯中的少量苯酚,应向混合物中加入NaOH溶液后分液,故A错误;
B.苯酚为有机物,常温下,苯酚在水中的溶解度不大,当温度高于65℃时,能跟水以任意比例互溶,故B错误;
C.苯酚的酸性很弱,不能使指示剂变色,碳酸的酸性强于苯酚,所以也不可以与碳酸氢钠反应,故C错误;
D.苯酚是一种有毒的物质,能使蛋白质变性,其稀溶液可直接用作防腐剂和消毒剂,故D正确。
解答题1.
(1)工业废水与苯进入设备Ⅰ得到苯酚、苯的溶液与可以排放的无酚工业废水,说明在设备Ⅰ中进行的是萃取,利用苯与苯酚相似的结构互溶与水不溶,将苯酚从工业废水里提取出来,用分液的方法将下层的工业废水放出排放,上层的苯酚、苯混合液进入设备Ⅱ;萃取、分液必须用到的仪器名称叫分液漏斗;
(2)盛有苯酚、苯溶液的设备Ⅱ中注入氢氧化钠溶液,此时,具有酸性的苯酚跟氢氧化钠发生反应,生成苯酚钠和水,由设备Ⅱ进入设备Ⅲ的物质A是C6H5ONa,在设备Ⅱ中的液体分为两层,上层是苯层,下层是苯酚钠的水溶液,上层的苯通过管道送回设备Ⅰ中继续萃取工业废水中的苯酚,循环使用,下层的苯酚钠溶液进入设备(Ⅲ);在盛有苯酚钠溶液的设备Ⅲ中,通入过量的二氧化碳气,发生化学反应,生成苯酚和碳酸氢钠;
(3)依据碳酸性比苯酚的酸性强,弱酸盐与“强”酸发生的复分解反应,二氧化碳和苯酚钠反应生成苯酚,反应的方程式为C6H5ONa+CO2+H2O→C6H5OH+NaHCO3;
(4)盛有碳酸氢钠溶液的设备Ⅳ中,加入生石灰,生石灰与碳酸氢钠溶液里的水反应生成氢氧化钙,熟石灰和与碳酸氢钠发生复分解反应,生成沉淀;溶液与沉淀通过过滤分离;
(5)设备Ⅴ应是石灰窑,CaCO3高温分解所得的产品是氧化钙和二氧化碳,所得二氧化碳通入设备Ⅲ,反应所得氧化钙进入设备Ⅳ.在含苯酚工业废水提取苯酚的工艺流程中,苯、氧化钙、CO2、和NaOH理论上应当没有消耗,它们均可以循环使用。
2.根据有机化学中氧化反应的概念:从有机物分子中去掉氢原子的反应称为氧化反应。该变化过程符合这一特点,故属于氧化反应。
第八张
单选题
1.
假设醇的表达式为R﹣(OH)n,R﹣(OH)n+nNa→R﹣(ONa)n+( )H2,即 n﹣OH+nNa→n﹣ONa+(
)H2,即 n﹣OH+nNa→n﹣ONa+( )H2,由于氢气物质的量相等,那么羟基的物质的量相等,所以3N(﹣OHA)=6N(﹣OHB)=2N(﹣OH C),N(﹣OH A):N(﹣OH B):N(﹣OH C)=2:1:3,故选D。
)H2,由于氢气物质的量相等,那么羟基的物质的量相等,所以3N(﹣OHA)=6N(﹣OHB)=2N(﹣OH C),N(﹣OH A):N(﹣OH B):N(﹣OH C)=2:1:3,故选D。
①乙醇沸点低,易挥发,可以易被检测,与测定原理有关;②乙醇密度比水小,可与水以任意比混溶,与测定原理无关;③乙醇分子中含有羟基,具有还原性,K2Cr2O7具有强氧化性,可以把乙醇迅速氧化为乙酸蓝绿色的Cr3+,与测定原理有关;④乙醇可看成是乙烷中的氢原子被羟基取代后的产物,是烃的含氧化合物,与测定原理无关,对乙醇的描述与此测定原理有关的是①③,故选C。
3.A.料酒的主要成分是乙醇,食醋的主要成分是乙酸,故A正确;
B.乙醇分子之间、乙酸分子之间都存在氢键,乙醇和乙酸常温下为液体,C2H6、C2H4常温下为气体,乙醇和乙酸的沸点和熔点都比C2H6、C2H4的沸点和熔点高,故B正确;
C.乙醇可以发生催化氧化,乙醇与乙酸都可以燃烧,燃烧属于氧化反应,故C正确;
D.乙醇和乙酸之间发生酯化反应生成乙酸乙酯,皂化反应是在碱性条件下进行的水解反应生成高级脂肪酸盐与水,与酯化反应的条件不同,物质不同,二者不互为逆反应,故D错误。
4.A.CH3OH不能发生消去反应,能发生催化氧化反应生成甲醛,故A错误;
B.(CH3CH2)2CHCH2OH,既能发生消去反应生成烯烃,又能发生催化氧化反应生成醛,故B正确;
C.(CH3CH2)3CCH2OH,与羟基相连的C有两个氢原子,能够被催化氧化成醛;与羟基相邻的C上没有氢原子,不能发生消去反应生成烯烃,故C错误;
D、(CH3CH2)3COH,与羟基相连的C没有氢原子上没有氢原子,不能够被催化氧化,故D错误。
5.乙二醇的物质的量为:0.25mol•L﹣1×0.02L=0.005mol,高锰酸钾的物质的量为:0.50mol•L﹣1×0.02L=0.01mol,该反应中氧化剂是高锰酸钾,乙二醇是还原剂,设乙二醇的氧化产物中碳元素的平均化合价为x,
根据电子守恒:氧化剂的物质的量×(7﹣2)=还原剂的物质的量×[x﹣(﹣1)]0.01mol×5=0.005mol×2×(x+1),x=4,即乙二醇的氧化产物中碳元素的平均化合价为+4价,
A、HOCH2﹣CHO中碳元素的平均化合价为0价,故A错误;
B、OHC﹣CHO中碳元素的平均化合价为+1价,故B错误;
C、HOOC﹣CHO中碳元素的平均化合价为+2价,故C错误;
D、CO2中碳元素的化合价是+4价,故D正确。
6.A、金属钠和水反应生成后氢氧化钠和氢气,钠还可以和乙醇反应,置换羟基中的氢,生成乙醇钠和氢气,所以不能利用金属钠检验.可以用无水硫酸铜,故A错误;
B、有机酸和醇脱水发生酯化反应生成酯,低级酯是有芳香气味的液体,可用作糖果、化妆品中的香料,故B正确;
C、蛋白质属于天然有机高分子化合物,在酸、碱和酶的作用下发生水解,水解的最终产物是氨基酸,故C正确;
D、乙烯是一种不饱和烃,含有碳碳双键,能发生加聚反应生成聚乙烯,聚乙烯性质坚韧,低温时人保持柔软性,性质稳定,所以聚乙烯塑料可用来制造多种包装材料,故D正确。
7.本题隐含的“陷阱”是醇在一定条件下脱水有两种方式;CH3OH不能发生分子内脱水;醇分子间脱水时,既可以是同种分子间,也可以是不同分子间。忽视任何一点均会导致错选。组成为CH4O和C3H8O的混合物最多由三种醇混合而成:CH3OH、CH3CH2CH2OH、(CH3)2CHOH,由于CH3OH不能发生消去反应,而CH3CH2CH2OH、(CH3)2CHOH消去产物相同,所以,它们的消去产物只有一种(丙烯);当它们发生分子间脱水时,由于同种醇与不同种醇之间均可发生分子间脱水,故可得六种醚。共得到7种产物。
8.分子式为C12H18O4,A错;乙醇的同系物应该是饱和一元醇,B错;该化合物分子中有碳碳双键和醇羟基,易被氧化,C正确;乙烯分子中的6个原子都在同一平面内,因此在含有碳碳双键的有机物分子中处于同一平面的原子至少有6个,D错。
9.由题目给出的信息可知:丙二醇的物理性质有:①无色粘稠状的透明液体,②无味,④沸点245℃,⑤熔点﹣6.5℃;化学性质有:③易燃⑥无腐蚀性⑦可用做水果催熟剂,故选A。
10.因三种醇与钠反应放出等量的氢气,三种醇提供的羟基数相等,设需要﹣OH的物质的量为nmol,而乙醇、乙二醇、甘油含有的羟基数分别为1、2、3,则三种醇的物质的量之比为nmol: nmol:
nmol: nmol=6:3:2,故选A。
nmol=6:3:2,故选A。
A.由结构式可以看出,木糖醇含有5个C,5个﹣OH,并且每个C原子上连接她个﹣OH,属于五元醇,故A正确;
B.木糖醇不是糖,但有甜味,属于无糖型植物甜味剂,故B正确;
C.单糖是不能水解的多羟基醛或多羟基酮,木糖醇不含有醛基或酮基,不是单糖,故C错误;
D.木糖醇分子中含有多个羟基可以分子内脱水生成环醚,故D正确。
12.A.乙醇可以通过粮食、秸杆发酵生成,也可以通过乙烯和水合成,所以乙醇是一种可再生能源,故A正确;
B.汽油、柴油的主要成分是碳氢化合物,植物油主要成分是油脂,故B错误;
C.苯分子中没有碳碳双键,不能使酸性的KMnO4溶液褪色,故C错误;
D.石油的分馏不能得到甲烷、乙烯等,只能的到汽油、煤油、柴油等轻质油和重油,然后轻质油再经过裂解可以得到甲烷、乙烯等小分子烃,故D错误。
13.A.乙醇可以通过粮食、秸杆发酵生成,也可以通过乙烯和水合成,所以乙醇是一种可再生能源,故A正确;
B.汽油、柴油的主要成分是碳氢化合物,植物油主要成分是油脂,故B错误;
C.苯分子中没有碳碳双键,不能使酸性的KMnO4溶液褪色,故C错误;
D.石油的分馏不能得到甲烷、乙烯等,只能的到汽油、煤油、柴油等轻质油和重油,然后轻质油再经过裂解可以得到甲烷、乙烯等小分子烃,故D错误。
14.A. 与羟基相连的碳原子上有氢原子,能发生催化氧化,可生成丁酮,故A不选;
与羟基相连的碳原子上有氢原子,能发生催化氧化,可生成丁酮,故A不选;
B.CH3CH2CH2OH与羟基相连的碳原子上有氢原子,能发生催化氧化,可生成丙醛,故B不选;
C. 与羟基相连的碳原子上有氢原子,能发生催化氧化,可生成醛酮,故C不选;
与羟基相连的碳原子上有氢原子,能发生催化氧化,可生成醛酮,故C不选;
D. 与羟基相连的相邻碳原子上没有氢原子,不能发生催化氧化,故D选。
与羟基相连的相邻碳原子上没有氢原子,不能发生催化氧化,故D选。
1.
(1)乙醇的催化氧化反应过程:金属铜被氧气氧化为氧化铜,2Cu+O2 2CuO,氧化铜将乙醇氧化为乙醛,CH3CH2OH+CuO
2CuO,氧化铜将乙醇氧化为乙醛,CH3CH2OH+CuO CH3CHO+Cu+H2O,反应需要加热进行,停止加热反应仍继续进行,说明乙醇的氧化反应是放热反应;
CH3CHO+Cu+H2O,反应需要加热进行,停止加热反应仍继续进行,说明乙醇的氧化反应是放热反应;
(2)甲和乙两个水浴作用不相同,甲是热水浴,作用是乙醇平稳气化成乙醇蒸气,乙是冷水浴,目的是将乙醛冷却下来,故答案为:加热乙醇,便于乙醇的挥发;冷却,便于乙醛的收集;
(3)乙醇被氧化为乙醛,同时生成水,反应乙醇不能完全反应,故a中冷却收集的物质有乙醛、乙醇与水;空气中氧气反应,集气瓶中收集的气体主要是氮气;
(4)若试管a中收集到的液体用紫色石蕊试纸检验,试纸显红色,说明液体中还含有乙酸,四个选择答案中,只有碳酸氢钠可以和乙酸反应,生成乙酸钠、水和二氧化碳,实现两种互溶物质的分离用蒸馏法。
2.烯烃可以由醇脱水或卤代烃与NaOH的醇溶液共热发生消去反应制得。饱和一元醇脱水可得到只有一个双键的单烯烃,若制取二烯烃,则应用二元醇脱水制得。涉及到的各步反应为

第九张
单选题
1. C
2. B
3. D
4. C
5. A
6. D
7. B
8. D
9. B
10. C
11. C
12. D
13. C
14. D
15. A
16. B
17. A
18. A
解答题
1.
(1)2,3-二甲基-2-丁烯;液
(2)(CH3)2CBrCBr(CH3)2+2NaOH 
 +2NaBr+2H2O
+2NaBr+2H2O
(3)n  →
→ 
(4)a
2. (1)CH3CH2Br+NaOH  CH3CH2OH+NaBr;不合理,未用硝酸中和氢氧化钠(未排除氢氧根离子的干扰)
CH3CH2OH+NaBr;不合理,未用硝酸中和氢氧化钠(未排除氢氧根离子的干扰)
(2)CH3CH2Br+NaOH  CH2==CH2↑+NaBr+H2O;高锰酸钾溶液褪色
CH2==CH2↑+NaBr+H2O;高锰酸钾溶液褪色
(3)吸收乙醇;
(1)2
(2)
(3)
(4) +Cl2
+Cl2 

第十张
单选题
1. C
2. D
3. C
4. B
5. C
6. D
7. D
8. C
9. C
10. C
11. B
12. D
13. C
解答题
1.
(1)CH2=CH2
(2)褪色
(3)C
(4)1
2.(1)2-甲基-2-丁烯
(2) E B C F
(3)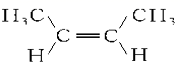
(4)CH3C≡CH + 2Br2 → CH3CBr2CHBr2
(5)4
3.(1)催化剂
(2)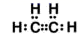
(3)nCH2=CH2

(4)AC
(5) 紫色褪去 CH2=CH2+Br2→CH2BrCH2Br
第十一张
单选题
1. A
2. C
3. B
4. D
5. C
6. B
7. C
8. A
9. B
10. D
11. C
12. B
13. B
14. A
15. A
16. C
17. B
18. D
19. A
解答题
1.
(1)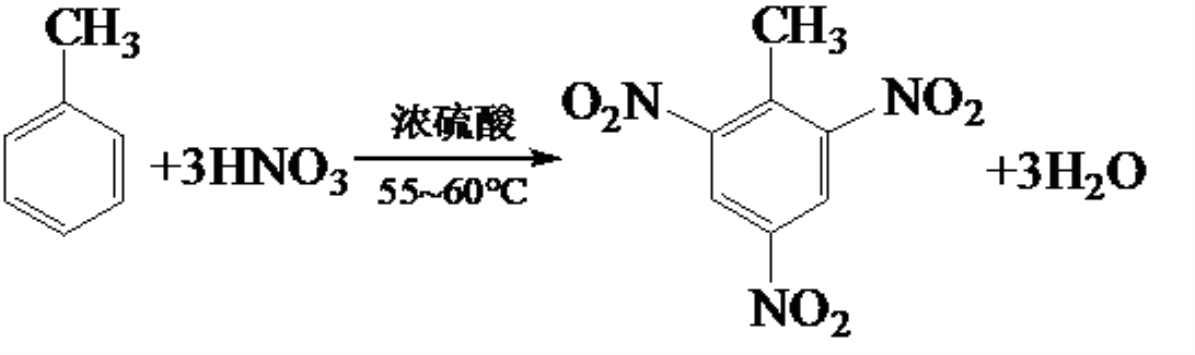
(2) 
(3)2CH3CH(OH)CH2CH3+O2
2CH3COCH2CH3+2H2O
(4)
(1)CH2OHCH(OH)CH2OH (2)变性
(3) 
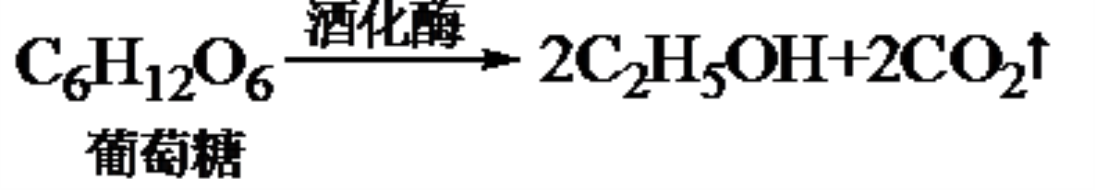
(4)①C13H16O5 ②bc
3.(1)加成反应或还原反应
(2)
(3)CH3COONa
(4)4 HOOCCH2CH2CH2COOH
4.(1)加成反应或还原反应
(2)
(3)CH3COONa
(4)4 HOOCCH2CH2CH2COOH
5.(1) (2)消去
(2)消去
(3) 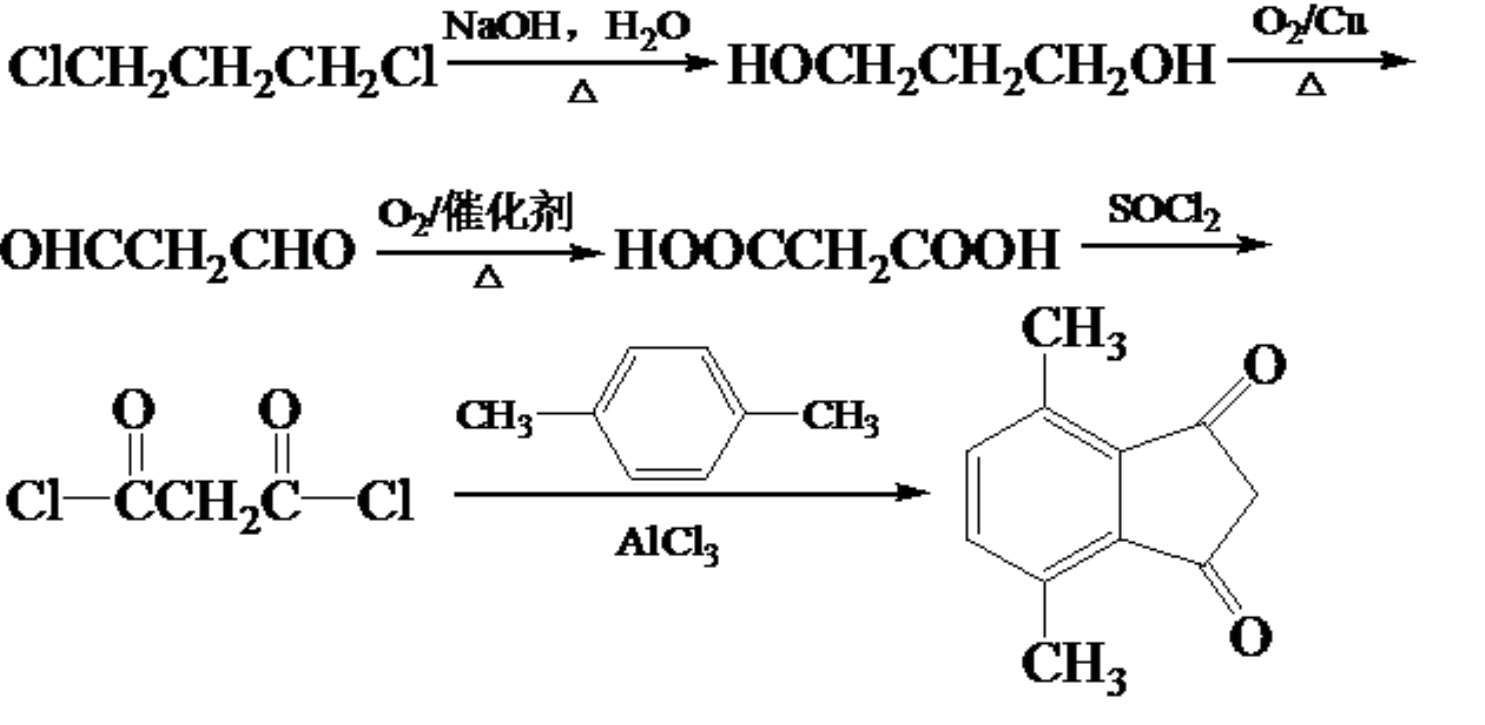
第十二张
单选题
1. B
2. A
3. B
4. C
5. C
6. C
7. B
8. D
9. D
10. D
11. C
12. D
13. C
14. A
15. B
16. B
17. D
18. B
19. D
20. A
解答题
1.
(1)② (2)⑤ (3)④ (4)① (5)③
2.(1)C和E
(2)
(3)C
(4) 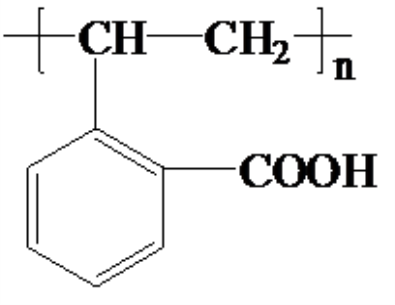
I.(1)N(C):N(H):N(O)=2:6:1 (2)C2H6O
(3)CH3OCH3 CH3CH2OH (4) CH3CH2OH
(5) 
(6)加成反应
(7)

II.(1)C7H6O3 CH3COOH
(2)
I.(1)N(C):N(H):N(O)=2:6:1 (2)C2H6O
(3)CH3OCH3 CH3CH2OH (4) CH3CH2OH
(5) 
(6)加成反应
(7)

II.(1)C7H6O3 CH3COOH
(2)
(1)苯酚 OHCCOOH
(2)③>①>②
(3) 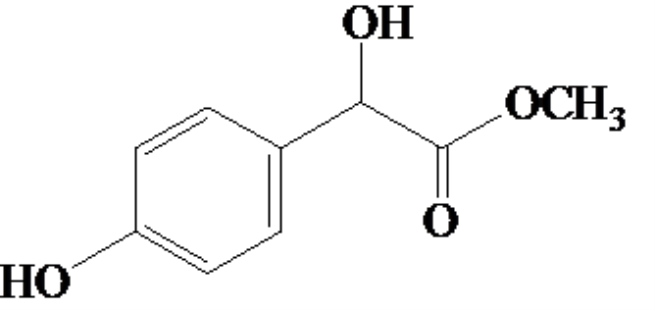
(4)3
(5) 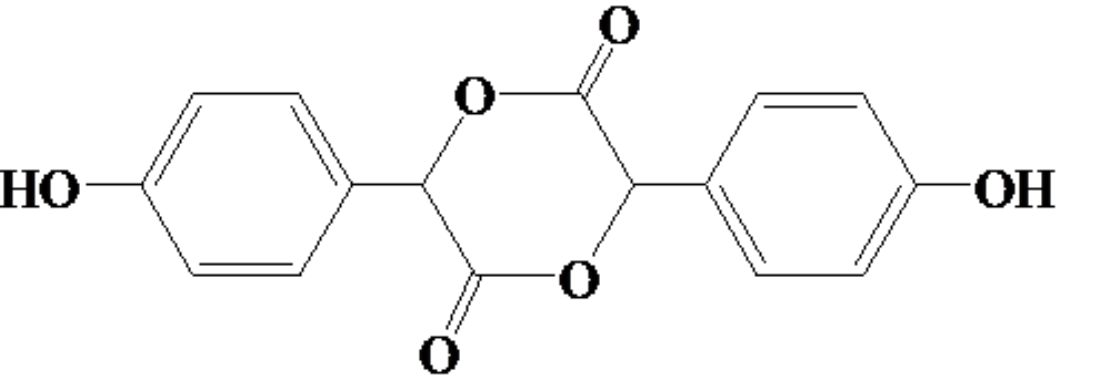 或
或

(1)C3H6 消去反应
(2)1,2-二溴丙烷 羰基 羧基
(3) 
(4)4 OHCCH2CH2CH2CHO
(5)